题目描述

给你一个二维字符网格数组 grid，大小为 m x n，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 相同的值。

同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true，否则返回 false。

样例

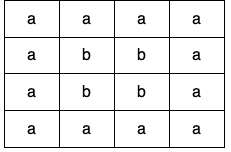
输入：
grid = [
        ["a","a","a","a"],
        ["a","b","b","a"],
        ["a","b","b","a"],
        ["a","a","a","a"]
    ]
输出：true
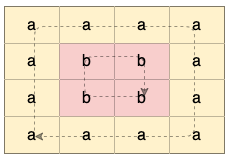
解释：如下图所示，有 2 个用不同颜色标出来的环：

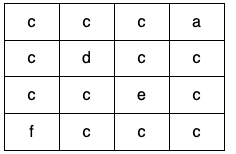
输入：
grid = [
        ["c","c","c","a"],
        ["c","d","c","c"],
        ["c","c","e","c"],
        ["f","c","c","c"]
    ]
输出：true
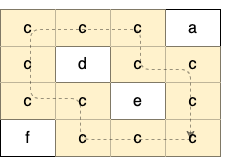
解释：如下图所示，只有高亮所示的一个合法环：

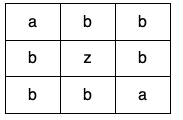
输入：
grid = [
        ["a","b","b"],
        ["b","z","b"],
        ["b","b","a"]
    ]
输出：false

限制

• m == grid.length
• n == grid[i].length
• 1 <= m <= 500
• 1 <= n <= 500
• grid 只包含小写英文字母。

算法1

(深度优先搜索) $O(mn)$

1. 一开始所有的位置都标记为未访问。
2. 从一个未访问的点开始深度优先搜索，将当前点的状态标记为访问中，考虑四周相同字符的点，都考虑结束后将当前的标记为已访问。
   • 如果相邻点为未访问，则递归访问这个点。
   • 如果相邻点为访问中，则可以忽略。这是因为我们遇到的是一个正在访问的点，不确定这个相邻点点是当前点的父节点还是一个合法的环点。
   • 如果相邻点为已访问，则返回 true，说明已经找到了一个环。这是因为从当前点开始，已经有两条路径到达这个相邻点，其中一条的长度肯定大于等于 3（因为其余的路径至少需要经过两个中间点），剩下的一条路径长度为 1（因为相邻）。因此，这说明找到了一个环。

时间复杂度

• 每个点的状态从未访问，变为访问中最后变为已访问，故总时间复杂度为 $O(mn)$。

空间复杂度

• 需要 $O(mn)$ 的额外空间存储状态数组和系统栈。

Go 代码

const (
    unvisited = iota
    visiting
    visited
)

var status [][]int
var m, n int

var dx = [4]int{0, 1, 0, -1}
var dy = [4]int{1, 0, -1, 0}

func dfs(x, y int, grid [][]byte) bool {
    status[x][y] = visiting

    for i := 0; i < 4; i++ {
        nx, ny := x+dx[i], y+dy[i]
        if nx < 0 || nx >= m || ny < 0 || ny >= n ||
            grid[nx][ny] != grid[x][y] || status[nx][ny] == visiting {
            continue
        }

        if status[nx][ny] == visited || dfs(nx, ny, grid) {
            return true
        }
    }

    status[x][y] = visited

    return false
}

func containsCycle(grid [][]byte) bool {
    m = len(grid)
    n = len(grid[0])
    status = make([][]int, m)
    for i := 0; i < m; i++ {
        status[i] = make([]int, n)
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if status[i][j] == unvisited {
                if dfs(i, j, grid) {
                    return true
                }
            }
        }
    }

    return false
}

算法2

(深度优先搜索) $O(mn)$

1. 类似于算法 1，只不过这里显式地记录了每个点访问的时间戳。
2. 一开始所有的位置都标记为 0。
3. 从一个未访问的点开始深度优先搜索，时间从 1 开始，记录当前的时间戳。考虑四周相同字符的点。
   • 如果相邻点时间戳不为 0，若此时当前时间与这个相邻点的时间戳的差值大于等于 3，说明找到了一条长度至少为 4 的环。
   • 如果相邻点时间戳为 0，递归访问，时间加 1。

时间复杂度

• 每个点仅被访问一次，故总时间复杂度为 $O(mn)$。

空间复杂度

• 需要 $O(mn)$ 的额外空间存储状态数组和系统栈。

Go 代码

var ts [][]int
var m, n int

var dx = [4]int{0, 1, 0, -1}
var dy = [4]int{1, 0, -1, 0}

func dfs(x, y, t int, grid [][]byte) bool {
    ts[x][y] = t

    for i := 0; i < 4; i++ {
        nx, ny := x+dx[i], y+dy[i]
        if nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] != grid[x][y] {
            continue
        }

        if ts[nx][ny] > 0 {
            if t-ts[nx][ny] >= 3 {
                return true
            }
            continue
        }

        if dfs(nx, ny, t+1, grid) {
            return true
        }
    }

    return false
}

func containsCycle(grid [][]byte) bool {
    m = len(grid)
    n = len(grid[0])
    ts = make([][]int, m)
    for i := 0; i < m; i++ {
        ts[i] = make([]int, n)
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if ts[i][j] == 0 {
                if dfs(i, j, 1, grid) {
                    return true
                }
            }
        }
    }

    return false
}