题目描述

给定一个整数 n 和一个整数数组 rounds。有一条圆形赛道由 n 个扇区组成，扇区编号从 1 到 n。现将在这条赛道上举办一场马拉松比赛，该马拉松全程由 m 个阶段组成。其中，第 i 个阶段将会从扇区 rounds[i - 1] 开始，到扇区 rounds[i] 结束。举例来说，第 1 阶段从 rounds[0] 开始，到 rounds[1] 结束。

请你以数组形式返回经过次数最多的那几个扇区，按扇区编号 升序 排列。

注意，赛道按扇区编号升序逆时针形成一个圆（请参见第一个示例）。

样例

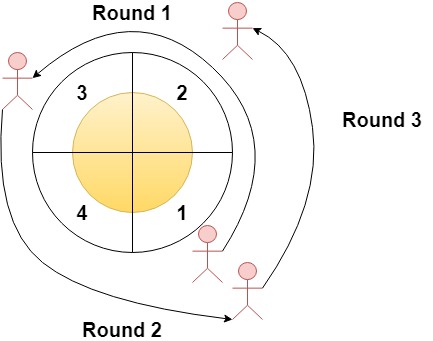
输入：n = 4, rounds = [1,3,1,2]
输出：[1,2]
解释：本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示：
1 --> 2 --> 3（阶段 1 结束）
  --> 4 --> 1（阶段 2 结束）
  --> 2（阶段 3 结束，即本场马拉松结束）
其中，扇区 1 和 2 都经过了两次，它们是经过次数最多的两个扇区。
扇区 3 和 4 都只经过了一次。

输入：n = 2, rounds = [2,1,2,1,2,1,2,1,2]
输出：[2]

输入：n = 7, rounds = [1,3,5,7]
输出：[1,2,3,4,5,6,7]

限制

• 2 <= n <= 100
• 1 <= m <= 100
• rounds.length == m + 1
• 1 <= rounds[i] <= n
• rounds[i] != rounds[i + 1]，其中 0 <= i < m

算法

(找规律) $O(n)$

1. 可以发现，最后的答案至于起始位置和终止位置有关。
2. 如果 st 小于等于 ed，则答案就是区间 [st, ed]。否则，答案就是区间 [1, ed] 并上 [st, n]。

时间复杂度

• 需要 $O(n)$ 的时间构造答案。

空间复杂度

• 需要 $O(n)$ 的额外空间存储答案。

Go 代码

func mostVisited(n int, rounds []int) []int {
    ans := make([]int, 0)
    st, ed := rounds[0], rounds[len(rounds)-1]

    if st > ed {
        for i := 1; i <= ed; i++ {
            ans = append(ans, i)
        }
        for i := st; i <= n; i++ {
            ans = append(ans, i)
        }
    } else {
        for i := st; i <= ed; i++ {
            ans = append(ans, i)
        }
    }

    return ans
}