算法1

(暴力) $O(nk)$

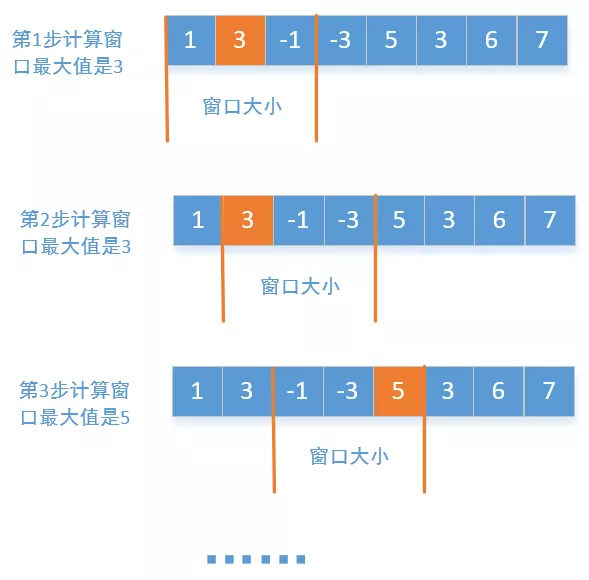
最简单的一种方式就是暴力求解，原理其实很简单，就是窗口在往右滑动的过程中，每滑动一步就计算窗口内的最大值。我们就以样例数据画个图来看下

Java 代码

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 边界条件判断
        if (nums == null || nums.length == 0) {
            return new int[0];
        } 

        int[] res = new int[nums.length - k + 1];
        for (int i = 0; i < res.length; ++i) {
            int max = nums[i];
            // 在每个窗口内找到最大值
            for (int j = 1; j < k; ++j) {
                max = Math.max(max, nums[i + j]);
            }
            res[i] = max;
        }
        return res;
    }
}

算法2

(双端队列) $O(n)$

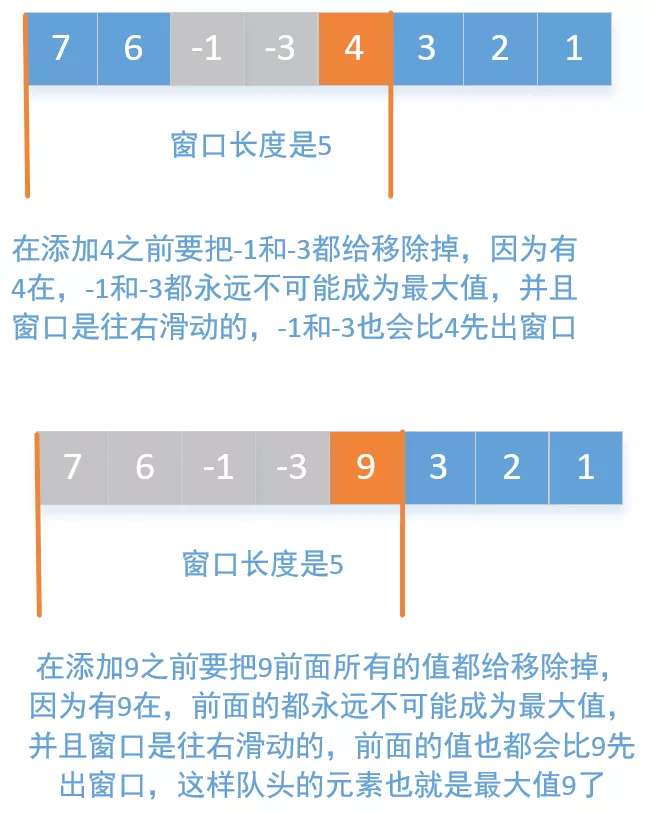
使用双端队列首先要搞懂一个问题，就是在双端队列中，要始终保证队头是队列中最大的值。那怎么保证呢，就是在添加一个值之前，比他小的都要被移除掉，然后再添加这个值。我们举个例子，比如窗口大小是$3$，双端队列中依次添加$3$个值$[4, 2, 5]$，在添加$5$之前我们要把$4$和$2$移除掉，让队列中只有一个$5$，因为窗口是往右滑动的，当添加$5$的时候，$4$和$2$都不可能再称为最大值了，并且$4$和$2$要比$5$还先出队列，搞懂了上面的过程我们随便画个图看下

Java 代码

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        // 边界条件的判断
        if (nums == null || k <= 0)
            return new int[0];

        int[] res = new int[nums.length - k + 1];
        int index = 0;

        // 双端队列，就是两边都可以插入和删除数据的队列，注意这里存储的是元素在数组中的下标，不是元素的值
        Deque<Integer> queue = new ArrayDeque<>();

        for (int i = 0; i < nums.length; ++i) {
            // 如果队列中队头元素和当前元素位置相差i-k，相当于队头元素要出窗口了，就把队头元素给移除
            // 注意队列中存储的是元素的下标（函数peekFirst()表示的是获取队头的下标，函数pollFirst()表示的
            // 是移除队头元素的下标）
            if (!queue.isEmpty() && queue.peekFirst() <= i - k) {
                queue.pollFirst();
            }
            // 在添加一个值之前，前面比他小的都要被移除掉，并且还要保证窗口中队头元素永远是队列中最大的
            while (!queue.isEmpty() && nums[queue.peekLast()] < nums[i]) {
                queue.pollLast();
            }
            // 当前元素的下标加入到队列的尾部
            queue.addLast(i);
            // 当窗口的长度大于等于k个的时候才开始计算(注意这里的i是从0开始的)
            if (i >= k - 1) {
                // 队头元素是队列中最大的，把队头元素加入到数组中
                res[index++] = nums[queue.peekFirst()];
            }
        }

        return res;
    }
}