题目简述

给 $n$ 个在第一象限坐标为整数的点，每个点表示以这个点为左下角的 $1\times 1$ 的正方形有一个物品。

需要寻找一个正方形，里面有不少于 $c$ 个物品，问正方形边长的最小值。

算法 $1$

暴力枚举。

枚举每一个正方形的左下角和边的长度。

时间复杂度 $O(m^3)$，其中 $m$ 是坐标的值域。

时间明显爆炸。

算法 $2$

首先观察符合条件边长的长度有单调性的。

$m$ 代表坐标的值域。

那么可以二分边长的长度。复杂度降为 $O(m^2\log m)$。

坐标的值域在 $[1,10000]$ 中，但坐标的数量最多只有 $500$，所以考虑离散化。

注意离散化的目的是降低值域的大小，同时保留点与点之间的位置关系。

如下图：

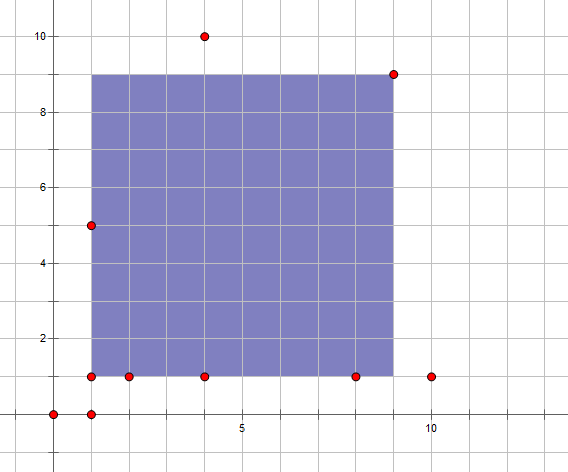
若 $n=8$，$c=5$，答案为 $8$。

离散化后：

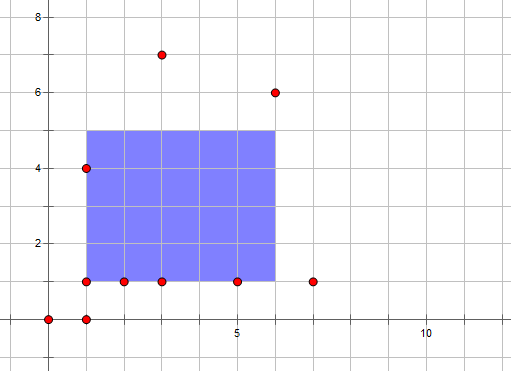
两图之间的关系大家可以仔细观察，笔者想了很久，没想出该怎么严谨地去说明离散化的方式。请读者在讨论教教笔者。

简单来说，对于点 $(x,y)$，要把它变为 $(x’,y’)$，其中 $x’$ 和 $y’$ 分别是 $x$ 和 $y$ 在点的横纵坐标的集合中从小到大第 $x’$ 和 $y’$ 名。这样的话，就实现了离散化的目的。

离散化后，前缀和预处理，二分边长，并判断是否可行。每次判断需要遍历一遍离散化后的点。

实现

可以发现思路很抽象。笔者是从别的题解自己琢磨出来的。所以来说一下实现的方法。

离散化：可以把 $x$ 和 $y$ 看作相同意义的数，放进一个容器进行排序并去重完成离散化。

$num$ 是点的横纵坐标的集合。

sort(num.begin(), num.end());
num.erase(unique(num.begin(), num.end()), num.end());

对于每个 $len$ 的判断：离散化后，需要遍历的矩形就是左下角为 $(1,1)$ 且右上角为 $(num.size()-1,num.size()-1)$。

for (int x2 = 1; x2 < num.size(); x2++) {
    while (num[x1] < num[x2] - len + 1) ++x1;
    y1 = 1;
    for (int y2 = 1; y2 < num.size(); y2++) { 
        while (num[y1] < num[y2] - len + 1) ++y1;
        if (sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] >= k) return 1;
    }
}

这样的遍历，就相当于遍历原先 $m\times m$ 的矩形每个点的坐标，只不过明显不会比其他点更好的点已略去，再把剩下的点离散化到一个更小的值域中。对应的，第 $k$ 个点到第 $k+1$ 个点的距离就是 $num[k+1]-num[k]$。

故遍历右上角的坐标，同时维护左下角的坐标，使左下角与右上角横坐标或纵坐标两者的差要小于 $len$ 的。

这样遍历的复杂度就降为 $O(n^2)$。

时间复杂度 $O(n^2\log m)$。

如有不足，请讨论或私信指出，谢谢。

C++ 代码

#include<bits/stdc++.h>

#define ll long long
#define y1 caibictq
#define P pair<int, int>
#define fi first
#define se second

using namespace std;

const int MAXN = 20010;
const int MAXM = 1010;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;

int n, m, k;
int tot, cnt, ans;

int read() {
    int f = 1, s = 0;
    char ch = getchar();
    while ('0' > ch || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
    while ('0' <= ch && ch <= '9') {s = (s << 1) + (s << 3) + ((int)ch ^ 48); ch = getchar();}
    return s * f;
}

int a[MAXN], b[MAXN];

vector<int> num;

int sum[MAXM][MAXM];

bool check(int len) {
    int x1, y1;
    x1 = 1;
    for (int x2 = 1; x2 < num.size(); x2++) {
        while (num[x1] < num[x2] - len + 1) ++x1;
        y1 = 1;
        for (int y2 = 1; y2 < num.size(); y2++) { 
            while (num[y1] < num[y2] - len + 1) ++y1;
            if (sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1] >= k) return 1;
        }
    }
    return 0;
}

struct Point {
    int x, y;
}p[MAXN];

int main() {
    int T;
    scanf("%d%d", &k, &n);
    num.push_back(0);
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &p[i].x, &p[i].y);
        num.push_back(p[i].x);
        num.push_back(p[i].y); 
    }
    sort(num.begin(), num.end());
    num.erase(unique(num.begin(), num.end()), num.end());
    for (int i = 1; i <= n; i++) {
        int x = lower_bound(num.begin(), num.end(), p[i].x) - num.begin();
        int y = lower_bound(num.begin(), num.end(), p[i].y) - num.begin();
        ++sum[x][y];
    }
    for (int i = 1; i < num.size(); i++) {
        for (int j = 1; j < num.size(); j++) {
            sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
        }
    }
    int l = 1, r = 10000, mid;
    while (l < r) {
        mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d\n", l);
    return 0;
}