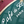题目特点： 边权为 0 或 1 的最短路径， 使用双端队列
按题意可知，
1. 如果连通，那么边权是0， 加入队列头部
2. 如果不连通， 边权是1， 加入队尾

注意点： bfs过程中, 普通bfs的是加入队头后就算到达最短距离
双端队列是出队了才算到达最短距离

性质， 最开始的衡纵坐标和是偶数， 题意是只能向斜的走，所以只能走到m + n和为偶数的点
如果m + n & 1 != 0, 是抵达不了的， 返回NO SOLUTION

本题还考察了一个映射关系

import java.io.*;
import java.util.*;
class Main{
    static BufferedReader read = new BufferedReader(new InputStreamReader(System.in));
    static int N = 510, INF = 0x3f3f3f3f, row, col;
    static char[][] g = new char[N][N];
    static boolean[][] st = new boolean[N][N];
    static int[][] dist = new int[N][N];
    static int[][] dir1 = new int[][]{{-1, -1}, {-1,1}, {1, 1}, {1, -1}}; // 映射关系1
    static int[][] dir2 = new int[][]{{-1, -1}, {-1, 0}, {0, 0}, {0, -1}}; // 映射关系2
    static char[] chars = new char[]{'\\', '/', '\\', '/'};

    public static void main(String[] args) throws Exception{

        int t = Integer.valueOf(read.readLine());

        while(t-- > 0){
            String[] ss = read.readLine().split(" ");
            row = Integer.valueOf(ss[0]); 
            col = Integer.valueOf(ss[1]);

            for(int i = 0; i < row; i++){
                String s = read.readLine();
                for(int j = 0; j < col; j++){
                    g[i][j] = s.charAt(j);
                }
            }

            if((row + col & 1) != 0) System.out.println("NO SOLUTION");
            else {
                System.out.println(bfs());
            }
        }
    }


    public static int bfs(){
        for(int i = 0; i <= row; i++)    {
            Arrays.fill(dist[i], INF);
            Arrays.fill(st[i], false);
        }
        dist[0][0] = 0;
        LinkedList<int[]> q = new LinkedList();
        q.offer(new int[]{0, 0});
        while(!q.isEmpty()){
            int[] poll = q.pollFirst();
            int x = poll[0], y = poll[1];
            if(x == row && y == col) return dist[x][y];

            if(st[x][y]) continue;
            st[x][y] = true;
            for(int i = 0; i < 4; i++){
                //格子能走的路
                int nx = x + dir1[i][0];
                int ny = y + dir1[i][1];
                if(nx < 0 || nx > row || ny < 0 || ny > col)    continue;
                if(st[nx][ny]) continue;
                //对应输入的 / 或 \
                int gx = x + dir2[i][0];
                int gy = y + dir2[i][1];
                int w = g[gx][gy] == chars[i] ? 0: 1;  //如果通路刚好相等为0， 不等为1
                int d = dist[x][y] + w;
                if(dist[nx][ny] > d){               
                    dist[nx][ny] = d;
                    if(w == 0){
                        q.addFirst(new int[]{nx, ny});
                    }else{
                        q.addLast(new int[]{nx, ny});
                    }
                }
            }
        }
        return -1;
    }
}