问题描述

Nearly every one have used the Multiplication Table. But could you find out the k-th smallest number quickly from the multiplication table?

Given the height m and the length n of a m * n Multiplication Table, and a positive integer k, you need to return the k-th smallest number in this table.
请你一个m * n的乘法表，请计算第k个小的元素。

举个例子：

解法1

先来看下乘法表每个元素的组成结构：

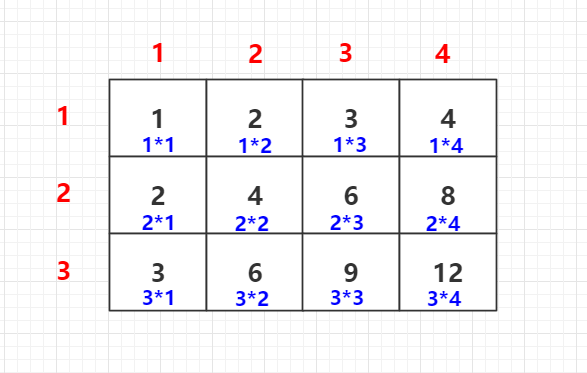
我们可以使用二分法，从上到下依次统计小于等于k元素的数量：

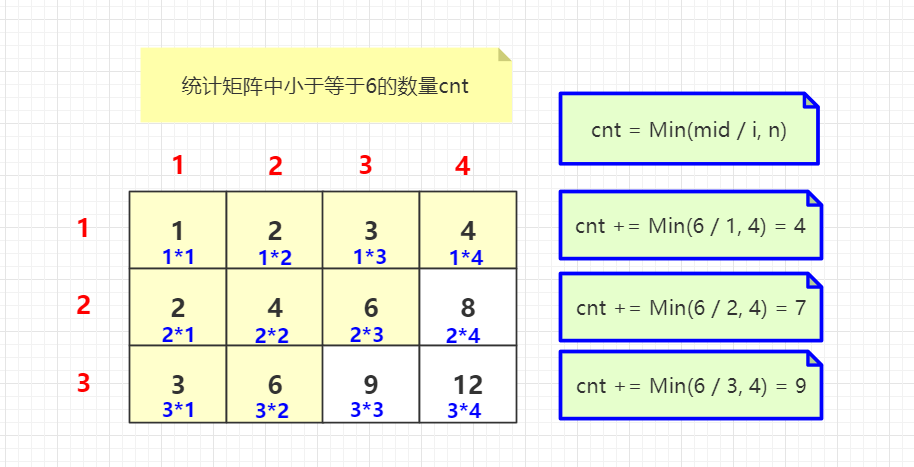
再来看下使用二分时满足的性质：

来看下实现：

class Solution {

    private int count(int m, int n, int mid){
        int cnt = 0;
        for (int i = 1; i <= m; i++){
            cnt += Math.min(mid / i, n);
        }
        return cnt;
    }

    public int findKthNumber(int m, int n, int k) {

        int l = 1, r = m * n;
        while (l < r){
            int mid = l + r >>> 1;
            if (count(m, n, mid) >= k) r = mid;
            else l = mid + 1;
        }
        return r;
    }
}

Enjoy it !

疑问

当我们使用这条性质时，m = 45, n = 12, k = 471，输出结果为311，正确结果为312

class Solution {

    private int count(int m, int n, int mid){
        int cnt = 0;
        for (int i = 1; i <= m; i++){
            cnt += Math.min(mid / i, n);
        }
        return cnt;
    }

    public int findKthNumber(int m, int n, int k) {

        int l = 1, r = m * n;
        while (l < r){
            int mid = l + r + 1 >>> 1;
            if (count(m, n, mid) <= k) l = mid;
            else r = mid - 1;
        }
        return r;
    }
}

若您知道如何调整，还请留言指点一下~