题目描述

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。

调用 next() 将返回二叉搜索树中的下一个最小的数。

样例

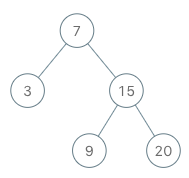
BSTIterator iterator = new BSTIterator(root);
iterator.next();    // 返回 3
iterator.next();    // 返回 7
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 9
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 15
iterator.hasNext(); // 返回 true
iterator.next();    // 返回 20
iterator.hasNext(); // 返回 false

提示：

• next() 和 hasNext() 操作的时间复杂度是 $O(1)$，并使用 $O(h)$ 内存，其中 h 是树的高度。
• 你可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 中至少存在一个下一个最小的数。

算法分析

• 1、二叉搜索树本身中序遍历后的元素是从小到大排序，因此找下一个最小的数，即在中序遍历中找当前元素的下一个元素
• 2、中序遍历的过程：将整课树的最左边一条链压入栈中，每次取出栈顶元素，并记录栈顶元素，如果它有右子树，则将右子树压入栈中。
• 3、此题是在中序遍历迭代手法的基础上进行拆分，首先先把整个左链键入到栈中，
  • next()操作：当前pop()出的栈顶元素就是下一个最小的元素，为了维护中序遍历的序列，因此需要把pop()出的栈顶元素的右儿子的左链的所有元素加入到依次栈中
  • hasNext()操作：判断栈是否有元素

时间复杂度 $O(1)$

Java 代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class BSTIterator {
    static Stack<TreeNode> stk = new Stack<TreeNode>();
    public BSTIterator(TreeNode root) {
        stk.clear();
        //将整个左链加入到栈中
        while(root != null)
        {
            stk.add(root);
            root = root.left;
        }
    }

    /** @return the next smallest number */
    public int next() {
        TreeNode p = stk.pop();
        int res = p.val;

        p = p.right;
        //将整个左链加入到栈中
        while(p != null)
        {
            stk.add(p);
            p = p.left;
        }
        return res;
    }

    /** @return whether we have a next smallest number */
    public boolean hasNext() {
        return !stk.isEmpty();
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */