题目描述

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

样例

输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，
     这笔交易所能获得利润 = 4-2 = 2 。

输入: [3,2,6,5,0,3], k = 2
输出: 7
解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 
     这笔交易所能获得利润 = 6-2 = 4 。
     随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 
     这笔交易所能获得利润 = 3-0 = 3 。

算法分析

状态机解法 AcWing 1057. 股票买卖 IV

如下是线性dp解法

首先，有个比较特殊的前提，若一共有n天，则最多买卖n/2次（因为买卖在同一天收益得0，买卖在不同天才会有收益），因此如果k > n/2的话，可以直接令k = n/2。

1、直接分析 $O(kn^2)$

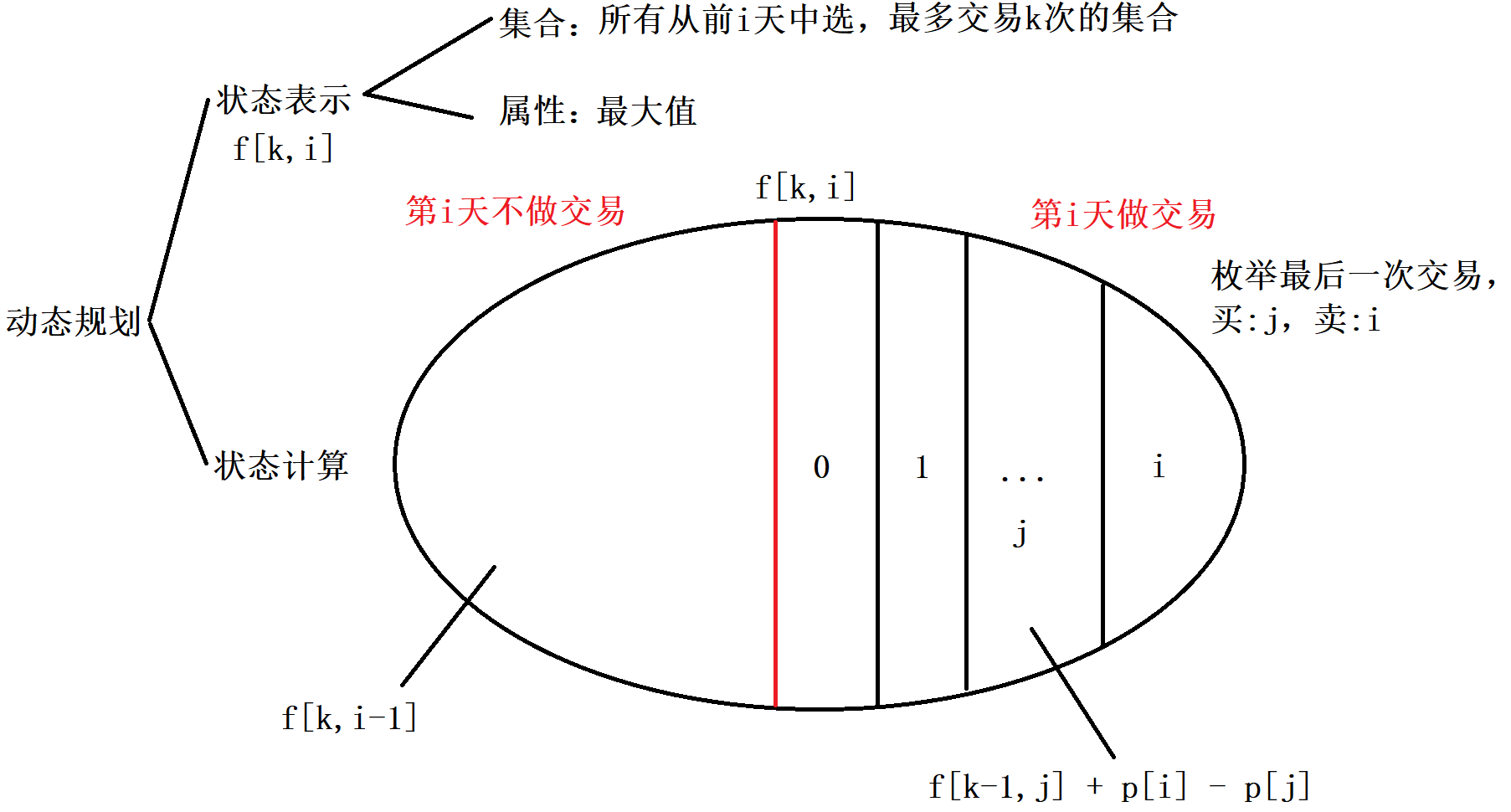
注意的是：即使最后一次买卖都是i，也不会影响结果

直接分析的 Java 代码 (会爆空间，爆时间)

class Solution {
    public int maxProfit(int K, int[] p) {
        int n = p.length;
        if(n == 0) return 0;
        K = Math.min(K, p.length / 2);
        int[][] f = new int[n + 10][n + 10];
        for(int k = 1;k <= K;k ++)
        {
            for(int i = 1;i < n;i ++)
            {
                f[k][i] = f[k][i - 1];
                for(int j = 0;j <= i;j ++)
                {
                    f[k][i] = Math.max(f[k][i], f[k - 1][j] + p[i] - p[j]);
                }
            }
        }
        return f[K][n - 1];
    }
}

2、优化时间

动态规划优化时间，往往从状态表达式中，对式子进行优化，即能不能把前面分析过的一堆东西不再重复分析，直接记录给下一次使用

由1中f[k, i]的状态表示细化如下所示

f[k, i] = max{ 
              f[k, i - 1],
              f[k - 1, 0] + p[i] - p[0]，
              f[k - 1, 1] + p[i] - p[1],
              ...
              f[k - 1, i - 1] + p[i] - p[i - 1],
              f[k - 1, i] + p[i] - p[i]
            }

即等价于 (交换p[i] 和 p[j]的位置)
f[k, i] = max{ 
              f[k, i - 1],
              f[k - 1, 0] - p[0] + p[i]，
              f[k - 1, 1] - p[1] + p[i],
              ...
              f[k - 1, i - 1] - p[i - 1] + p[i],
              f[k - 1, i] - p[i] + p[i]
            }

• 1、令 val = max(f[k - 1, j] - p[j]) ，0 <= j < i，由于这一个 val 可以由上一层传下来，初始化是 val = f[k - 1, 0] - p[0]
• 2、因此对于每次转移，只需要记录最大的 val 即可，因此f[k, i] = max{f[k, i - 1], val + p[i]}，并更新当前的val，即val = max(val, f[k - 1, i] - p[i])

优化时间的 Java 代码 （爆空间）

class Solution {
    public int maxProfit(int K, int[] p) {
        int n = p.length;
        if(n == 0) return 0;
        K = Math.min(K, p.length / 2);
        int[][] f = new int[n + 10][n + 10];
        for(int k = 1;k <= K;k ++)
        {
            int val = f[k - 1][0] - p[0];
            for(int i = 1;i < n;i ++)
            {
                f[k][i] = Math.max(f[k][i - 1], val + p[i]);
                val = Math.max(val, f[k - 1][i] - p[i]);
            }
        }
        return f[K][n - 1];
    }
}

3、优化空间

对于每次求f[k, i]时会发现，每次的状态方程只会用到f[k - 1,i]，即只会用到上一层，因此可以用滚动数组进行优化，共$2n$的空间，一数组用来记录f[k - 1,i]的结果，另一数组用来记录f[k,i]的结果

当前层是 k & 1，上一层是k - 1 & 1

将上面2的代码的k - 1以及k进行处理即可，如下所示

优化空间的 Java 代码 （什么都不爆）

class Solution {
    public int maxProfit(int K, int[] p) {
        int n = p.length;
        if(n == 0) return 0;
        K = Math.min(K, p.length / 2);
        int[][] f = new int[2][n + 10];
        for(int k = 1;k <= K;k ++)
        {
            int val = f[k - 1 & 1][0] - p[0];
            for(int i = 1;i < n;i ++)
            {
                f[k & 1][i] = Math.max(f[k & 1][i - 1], val + p[i]);
                val = Math.max(val, f[k - 1 & 1][i] - p[i]);
            }
        }
        return f[K & 1][n - 1];
    }
}

4、再次优化

可以发现一点是，当K >= p.length / 2时，其实就等价于可以买卖无限次，就是 LeetCode 122. 买卖股票的最佳时机 II 的问题，因此可以再次优化

再次优化后的代码

class Solution {
    public int maxProfit(int K, int[] p) {
        int n = p.length;
        if(n == 0) return 0;

        if (K >= p.length / 2) {
            int ans = 0;
            for(int i = 0;i < n - 1;i ++)
            {
                int d = p[i + 1] - p[i];
                if(d > 0) ans += d;
            }
            return ans ;
        }
        int[][] f = new int[2][n + 10];
        for(int k = 1;k <= K;k ++)
        {
            int val = f[k - 1 & 1][0] - p[0];
            for(int i = 1;i < n;i ++)
            {
                f[k & 1][i] = Math.max(f[k & 1][i - 1], val + p[i]);
                val = Math.max(val, f[k - 1 & 1][i] - p[i]);
            }
        }
        return f[K & 1][n - 1];
    }
}