题目描述

给定一个由若干 0 和 1 组成的二维网格 grid，其中 0 表示水，而 1 表示陆地。岛屿由水平方向或竖直方向上相邻的 1（陆地）连接形成。

如果 恰好只有一座岛屿，则认为陆地是 连通的；否则，陆地就是 分离的。

一天内，可以将任何单个陆地单元 1 更改为水单元 0。

返回使陆地分离的最少天数。

样例

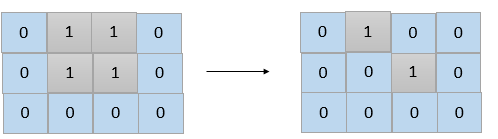
输入：grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]
输出：2
解释：至少需要 2 天才能得到分离的陆地。
将陆地 grid[1][1] 和 grid[0][2] 更改为水，得到两个分离的岛屿。

输入：grid = [[1,1]]
输出：2
解释：如果网格中都是水，也认为是分离的 ([[1,1]] -> [[0,0]])，0 岛屿。

输入：grid = [[1,0,1,0]]
输出：0

输入：grid = [[1,1,0,1,1],
             [1,1,1,1,1],
             [1,1,0,1,1],
             [1,1,0,1,1]]
输出：1

输入：grid = [[1,1,0,1,1],
             [1,1,1,1,1],
             [1,1,0,1,1],
             [1,1,1,1,1]]
输出：2

限制

• 1 <= grid.length, grid[i].length <= 30
• grid[i][j] 为 0 或 1。

算法

(图论) $O(mn)$

1. 答案只有可能是 0、1 或 2。这是因为一个足够大的陆地，必然存在一个点的度数为 2。
2. 答案为 0 的情况是陆地本身分离，或者就没有陆地。
3. 答案为 1 的情况为陆地的大小就是 1，或通过 tarjan 算法来判断陆地存在割点。
4. 剩余的情况都是 2。

时间复杂度

• 整张图的点数和边数都是 $O(mn)$ 的，所以 tarjan 算法的时间复杂度为 $O(mn)$。
• 判断逻辑可以依赖于 tarjan 的结果，所以总的时间复杂度也是 $O(mn)$。

空间复杂度

• 需要 $O(mn)$ 的额外空间存储 tarjan 算法所需要的数据结构。

C++ 代码

class Solution {
private:
    int m, n;
    int ts;
    vector<vector<int>> dfn, low;
    bool cut;
    int rx, ry;

    void dfs(int x, int y, const vector<vector<int>> &grid) {
        const int dx[4] = {0, 1, 0, -1};
        const int dy[4] = {1, 0, -1 ,0};

        dfn[x][y] = low[x][y] = ++ts;
        int branch = 0;
        for (int i = 0; i < 4; i++) {
            int tx = x + dx[i], ty = y + dy[i];
            if (tx < 0 || tx >= m || ty < 0 || ty >= n || grid[tx][ty] == 0)
                continue;

            if (dfn[tx][ty] != 0) {
                low[x][y] = min(low[x][y], dfn[tx][ty]);
                continue;
            }

            dfs(tx, ty, grid);

            branch++;
            low[x][y] = min(low[x][y], low[tx][ty]);

            if (low[tx][ty] >= dfn[x][y]) {
                if (branch >= 2 || !(x == rx && y == ry))
                    cut = true;
            }
        }
    }

public:
    int minDays(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        dfn.resize(m, vector<int>(n, 0));
        low.resize(m, vector<int>(n, 0));
        ts = 0;
        cut = false;

        bool first = false;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (grid[i][j] == 1 && dfn[i][j] == 0) {
                    if (first) return 0;
                    first = true;
                    rx = i; ry = j;
                    dfs(i, j, grid);
                }

        if (!first) return 0;
        if (ts == 1 || cut) return 1;
        return 2;
    }
};