题目描述

给定一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums 中的顺序依次插入一个初始为空的二叉查找树（BST）。请你统计将 nums 重新排序后，统计满足如下条件的方案数：重排后得到的二叉查找树与 nums 原本数字顺序得到的二叉查找树相同。

比方说，给定 nums = [2,1,3]，我们得到一棵 2 为根，1 为左孩子，3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST，但 [3,2,1] 会得到一棵不同的 BST。

请你返回重排 nums 后，与原数组 nums 得到相同二叉查找树的方案数。

由于答案可能会很大，请将结果对 10^9 + 7 取余数。

样例

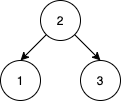
输入：nums = [2,1,3]
输出：1
解释：我们将 nums 重排，[2,3,1] 能得到相同的 BST。
没有其他得到相同 BST 的方案了。

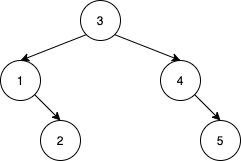
输入：nums = [3,4,5,1,2]
输出：5
解释：下面 5 个数组会得到相同的 BST：
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

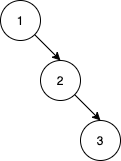
输入：nums = [1,2,3]
输出：0
解释：没有别的排列顺序能得到相同的 BST。

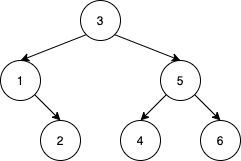
输入：nums = [3,1,2,5,4,6]
输出：19

输入：nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18]
输出：216212978
解释：得到相同 BST 的方案数是 3216212999。将它对 10^9 + 7 取余后得到 216212978。

限制

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= nums.length
• nums 中所有数 互不相同。

算法

(递归) $O(n^2)$

1. 分步计算，使用乘法原理。
2. 对于当前数组，显然第一个元素为根节点，然后剩下的元素需要按照与根节点的大小关系分配到 lo 和 hi 中。这一步中共有 n-1 个位置，其中需要选出 l = lo.size()（或 h = hi.size()）个位置，所以这一步的方案数为 $\binom{n-1}{l}$。
3. 之后，分别递归 lo 和 hi 数组，并将每一步的结果乘起来就是总方案数。
4. 总方案数减 1 就是答案。
5. 组合数计算既可以提前预处理，也可以通过阶乘数组与乘法逆元现场计算。

时间复杂度

• 每一层递归需要的时间为 $O(n)$，最坏情况下有 $O(n)$ 层，故总时间复杂度为 $O(n^2)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储系统栈，临时数组和阶乘数组。

C++ 代码

#define LL long long
const int mod = 1000000007;

class Solution {
private:
    vector<LL> fact;

    LL power(LL x, LL y) {
        LL tot = 1, p = x;
        for (; y; y >>= 1) {
            if (y & 1)
                tot = tot * p % mod;
            p = p * p % mod;
        }

        return tot;
    }

    LL select(int n, int m) {
        return fact[n] * power(fact[m], mod-2) % mod
                       * power(fact[n-m], mod-2) % mod;
    }

    int solve(const vector<int> &nums) {
        if (nums.size() == 0)
            return 1;

        vector<int> lo, hi;
        const int n = nums.size();

        for (int i = 1; i < n; i++) {
            if (nums[i] < nums[0]) lo.push_back(nums[i]);
            else hi.push_back(nums[i]);
        }

        return select(n-1, lo.size()) * solve(lo) % mod * solve(hi) % mod;
    }

public:
    int numOfWays(vector<int>& nums) {
        const int n = nums.size();
        fact.resize(n);
        fact[0] = 1;
        for (int i = 1; i < n; i++)
            fact[i] = fact[i - 1] * i % mod;

        return (solve(nums) - 1 + mod) % mod;
    }
};