在yxc老师的解法 上增加了图解，便于理解。

题目描述

给定两个有序数组 nums1 和 nums2，长度分别为 n,m.请找出它们的中位数，要求时间复杂度在 $O(log(n+m))$

样例

nums1 = [1, 3]
nums2 = [2]

中位数是 2.0

nums1 = [1, 2]
nums2 = [3, 4]

中位数是 (2 + 3) / 2 = 2.5

算法1

(递归) $O(log(n+m))$

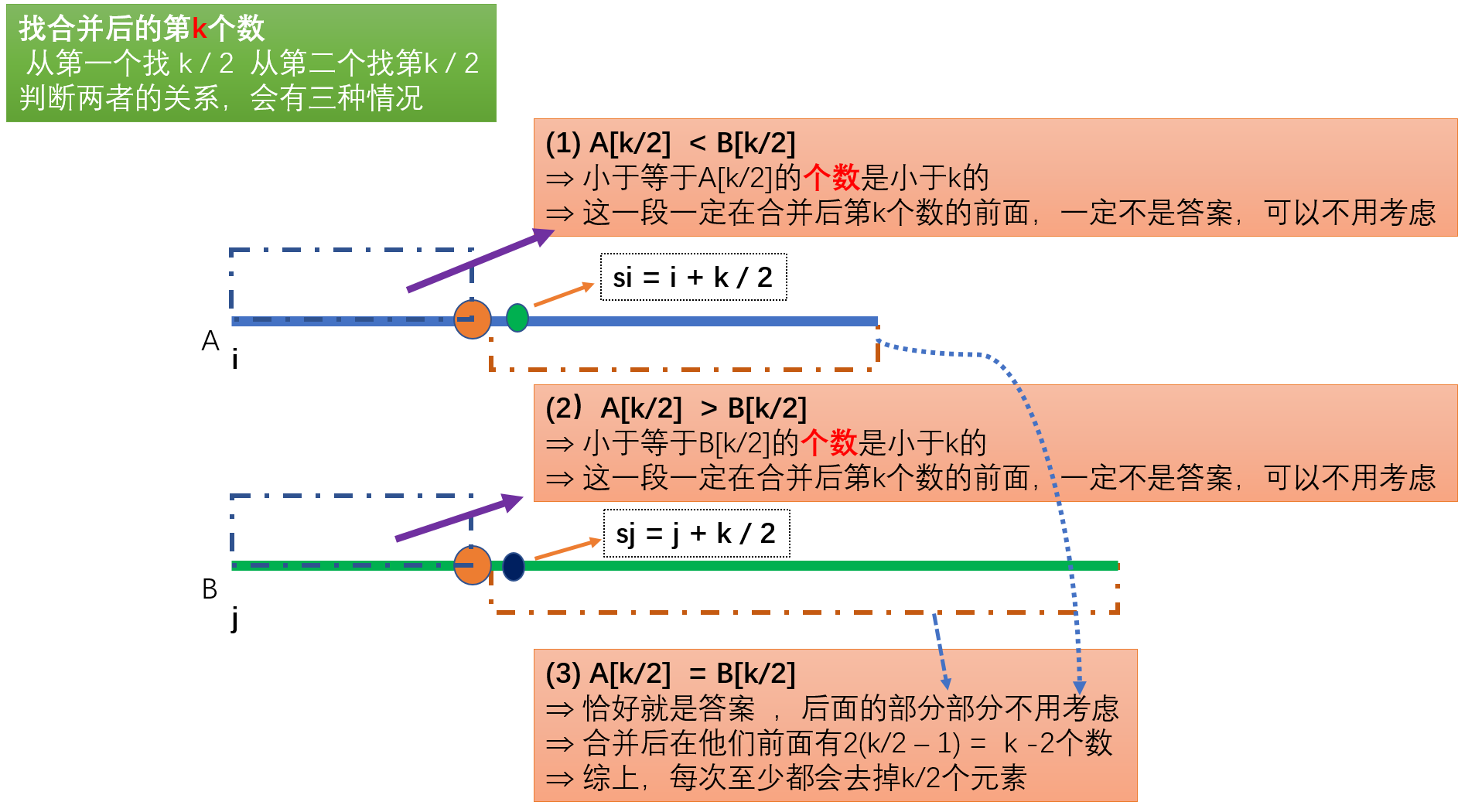
首先考虑下如何在两个有序数组，从小到大排序， 第k个数是多少
加入两个数组的长度分别为n, m,那么k = ( m+n) /2 即为所求

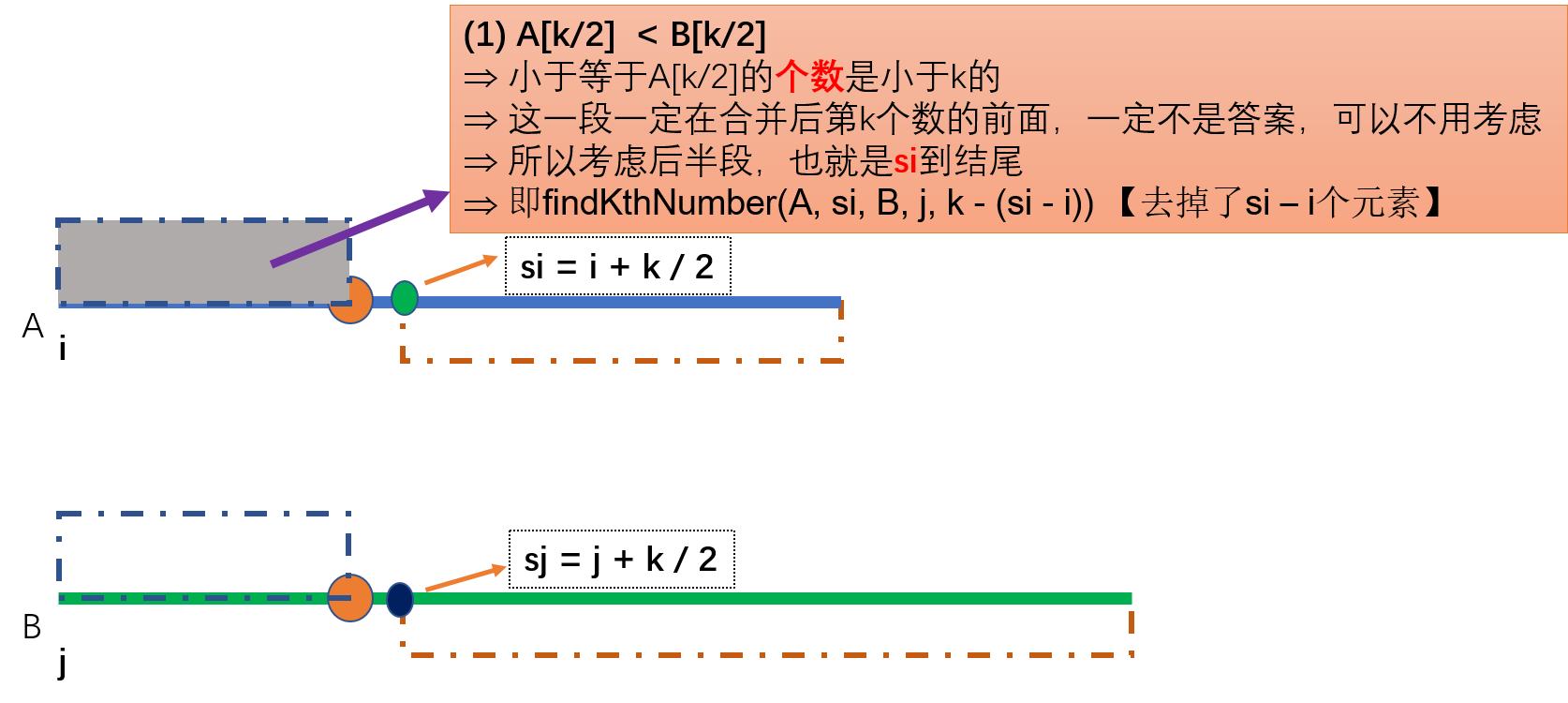
• A[k/2] < B[k/2]
  

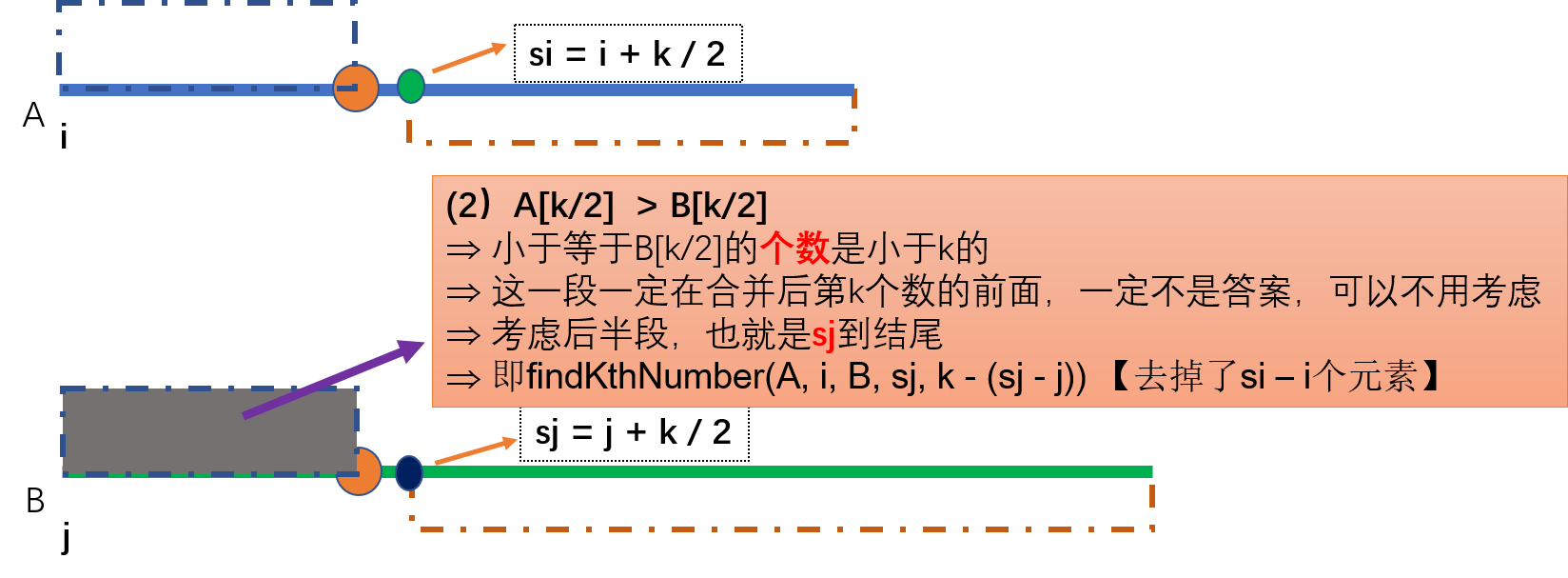
• A[k/2] > B[k/2]
  

时间复杂度

k=(m+n)/2，且每次递归 k的规模都减少一半，
因此时间复杂度是 $O(log(m+n))$.

参考文献

https://www.acwing.com/solution/content/50/

C++ 代码

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int tot = nums1.size() + nums2.size();
        // 偶数的话就是 2个平均数
        if (tot % 2 == 0){
            int left = findKthNumber(nums1, 0, nums2, 0, tot / 2);
            int right = findKthNumber(nums1, 0, nums2, 0, tot / 2 + 1);
            return (left + right) / 2.0;   // 记得 2.0
        }
        // 奇数的话返回 中间的数
        else
            return findKthNumber(nums1, 0, nums2, 0, tot / 2 + 1);

    }

    // i，j表示寻找的区间的起点下标
    // i 表示第一个数组从第i个数到最后，j表示第二个数组从 j 到最后。
    int findKthNumber(vector<int> &nums1, int i, vector<int> &nums2, int j, int k)
    {  
        // 方便处理 假定第一个数组比较短 个数少   但是也要注意其为空 越界的情况
        if (nums1.size() - i > nums2.size() - j)
            return findKthNumber(nums2, j, nums1, i, k);
        // 边界处理
        if (nums1.size() == i)  // 第一个数组为空
            return nums2[j + k - 1];  // k从1开始的 
        // 边界处理    
        if (k == 1) 
            return min(nums1[i], nums2[j]);

        int si = min(i + k / 2, int(nums1.size()));   // 坐标  第k/2和元素的下一个  所以下面要减1
        int sj = j + k / 2;                           // 坐标
        if (nums1[si - 1] > nums2[sj - 1])  // nums2的前半段没用  
             return findKthNumber(nums1, i, nums2, sj, k - (sj - j)); // 删除的个数 // sj - 1 - j + 1
        else  // // nums1的前半段没用
             return findKthNumber(nums1, si, nums2, j, k - (si - i));

    }
};