题目描述

几个人一起出去吃饭是常有的事。

但在结帐的时候，常常会出现一些争执。

现在有 n 个人出去吃饭，他们总共消费了 S 元。

其中第 i 个人带了 ai 元。

幸运的是，所有人带的钱的总数是足够付账的，但现在问题来了：每个人分别要出多少钱呢？

为了公平起见，我们希望在总付钱量恰好为 S 的前提下，最后每个人付的钱的标准差最小。

这里我们约定，每个人支付的钱数可以是任意非负实数，即可以不是 1 分钱的整数倍。

你需要输出最小的标准差是多少。

标准差的介绍：标准差是多个数与它们平均数差值的平方平均数，一般用于刻画这些数之间的“偏差有多大”。

形式化地说，设第 i 个人付的钱为 bi 元，那么标准差为 :

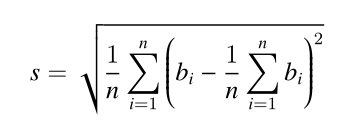
输入格式

第一行包含两个整数 n、S；

第二行包含 n 个非负整数 a1, …, an。

输出格式

输出最小的标准差，四舍五入保留 4 位小数。

数据范围

1≤n≤5×105,
0≤ai,S≤109

输入样例1：

5 2333
666 666 666 666 666

输出样例1：

0.0000

输入样例2：

10 30
2 1 4 7 4 8 3 6 4 7

输出样例2：

0.7928

主要考点

贪心

核心思想

从小到大排序, 钱不够平均值则掏出当前剩余的所有钱, 不够的部分后面均摊,
当前钱够的话则掏平均值的钱即可.

C ++ 代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>

using namespace std;
const int N = 5e5 + 10;

int n, s;
int a[N];

int main(){
    cin >> n >> s;
    for(int i = 0; i < n; i ++) cin >> a[i];

    sort(a, a + n);  //以防后面的前不够平均数但已无能补偿的情况

    double ave = 1.0 * s / n, cur_ave = ave, sum = 0;
    for(int i = 0; i < n; i ++){
        if(a[i] <= cur_ave){
            sum += (a[i] - ave) * (a[i] - ave);
            s -= a[i];
            cur_ave = 1.0 * s / (n - i - 1);
        }
        else{
            sum += (cur_ave - ave) * (cur_ave - ave);
        }
    }

    printf("%.4lf\n", sqrt(sum / n));

    return 0;
}