题目描述

给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。

样例

输入: "aacecaaa"
输出: "aaacecaaa"

输入: "abcd"
输出: "dcbabcd"

算法分析

kmp算法

• 1、找出题目中的等价条件
  

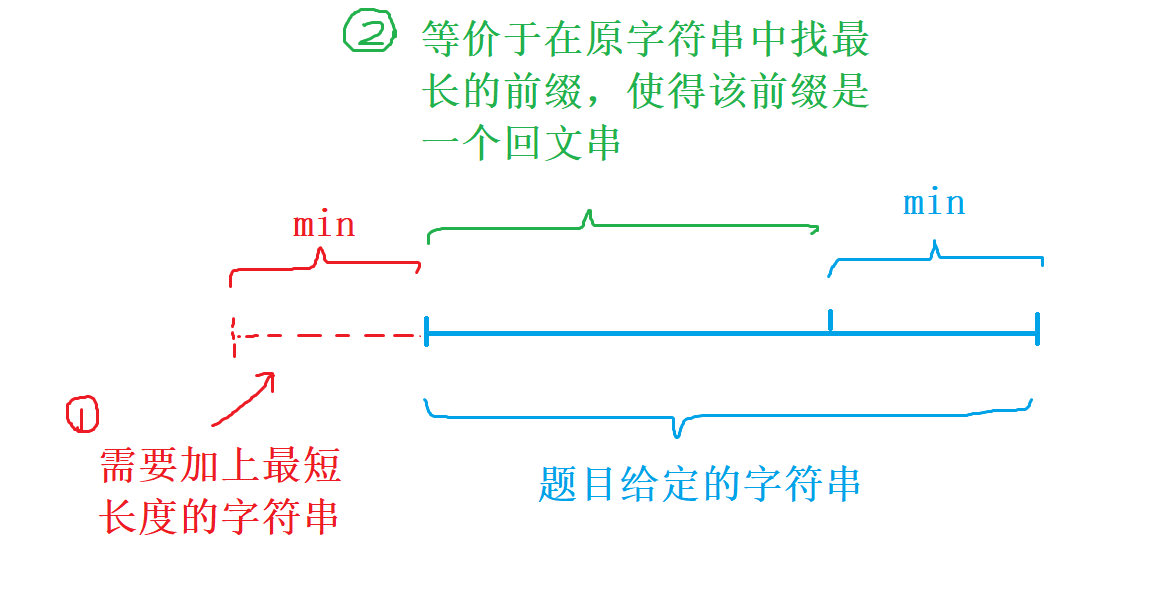
• 2、假设当前给定的字符串是s，将字符串s逆序复制一份t，将s + '#' + t作为新的字符串进行分析，其中'#'是s字符串中不可能出现的字符（此操作跳跃性高，一般想不出来）

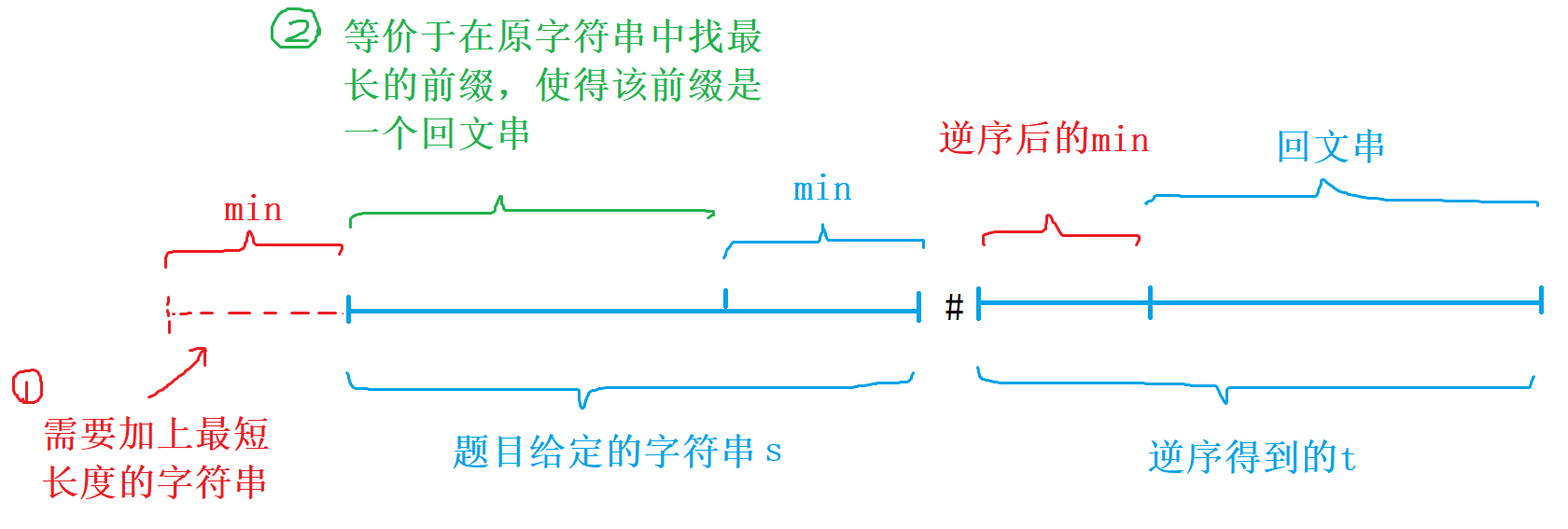
• 3、扩展后，此问题变成 求最大后缀等于最大前缀时的最大前缀末尾的位置，等价于用kmp算法中的next[]数组，求next[2 * n + 1]的值，其中2 * n + 1是末端的位置

• 4、找到了是一个回文串的最大前缀的末尾位置后，只需要将后面红色字逆序形成的min段left = [n + 2,2 * n + 2 - len - 1]放在原本的字符串前面即可，即答案是 left + 题目给定的字符串

时间复杂度 $O(n)$

Java 代码

bclass Solution {
    public String shortestPalindrome(String s) {
        int n = s.length();
        StringBuffer sb = new StringBuffer(s).reverse();
        s = " " + s + "#" + sb.toString();
        int[] ne = new int[2 * n + 2];
        for(int i = 2,j = 0;i <= 2 * n + 1;i ++)
        {
            while(j != 0 && s.charAt(i) != s.charAt(j + 1)) j = ne[j];
            if(s.charAt(i) == s.charAt(j + 1)) j ++;
            ne[i] = j;
        }
        int len = ne[2 * n + 1];
        String left = s.substring(n + 2, 2 * n + 2 - len);
        return left + s.substring(1, n + 1);
    }
}