题目描述

给出一个完全二叉树，求出该树的节点个数。

说明：

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

样例

输入: 
    1
   / \
  2   3
 / \  /
4  5 6

输出: 6

算法分析

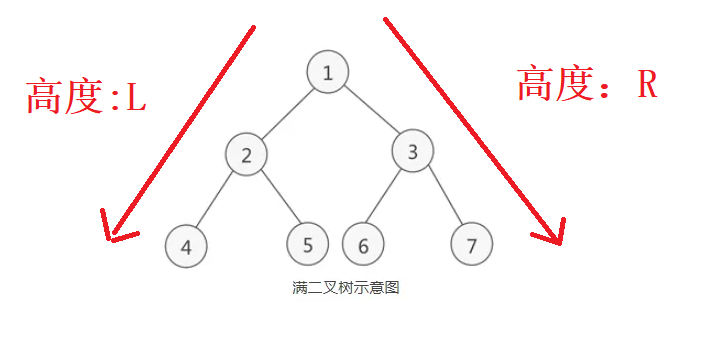
如图所示，当给定一棵满二叉树时(沿着左边一直走的深度是L，沿着右边一直走的深度是R，当L == R时是一棵满二叉树)，可以直接求出满二叉树的节点个数2^L - 1个节点

操作：

• 当当前树是一棵满二叉树时，则直接返回2^L - 1，否则需要递归求出左儿子的节点个数a，以及右儿子的节点个数b，返回总个数a + 1 + b

时间复杂度 $O(logn * logn)$

每次判断左右深度的时间复杂度是$O(logn)$，需要判断$O(logn)$次

Java 代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        TreeNode l = root, r = root;
        int x = 0, y = 0;
        while(l != null)
        {
            l = l.left;
            x ++;
        }
        while(r != null)
        {
            r = r.right;
            y ++;
        }
        if(x == y) return (1 << x) - 1;
        return countNodes(root.left) + 1 + countNodes(root.right);
    }
}