题目描述

在二维平面上计算出两个由直线构成的矩形重叠后形成的总面积。

每个矩形由其左下顶点和右上顶点坐标表示，如图所示。

样例

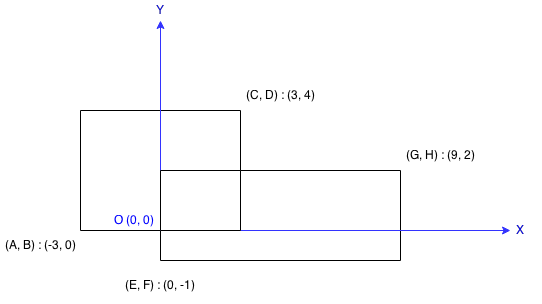
输入: -3, 0, 3, 4, 0, -1, 9, 2
输出: 45

说明: 假设矩形面积不会超出 int 的范围。

算法分析

如何找相交区域的左下角坐标和右上角坐标？

情况一：

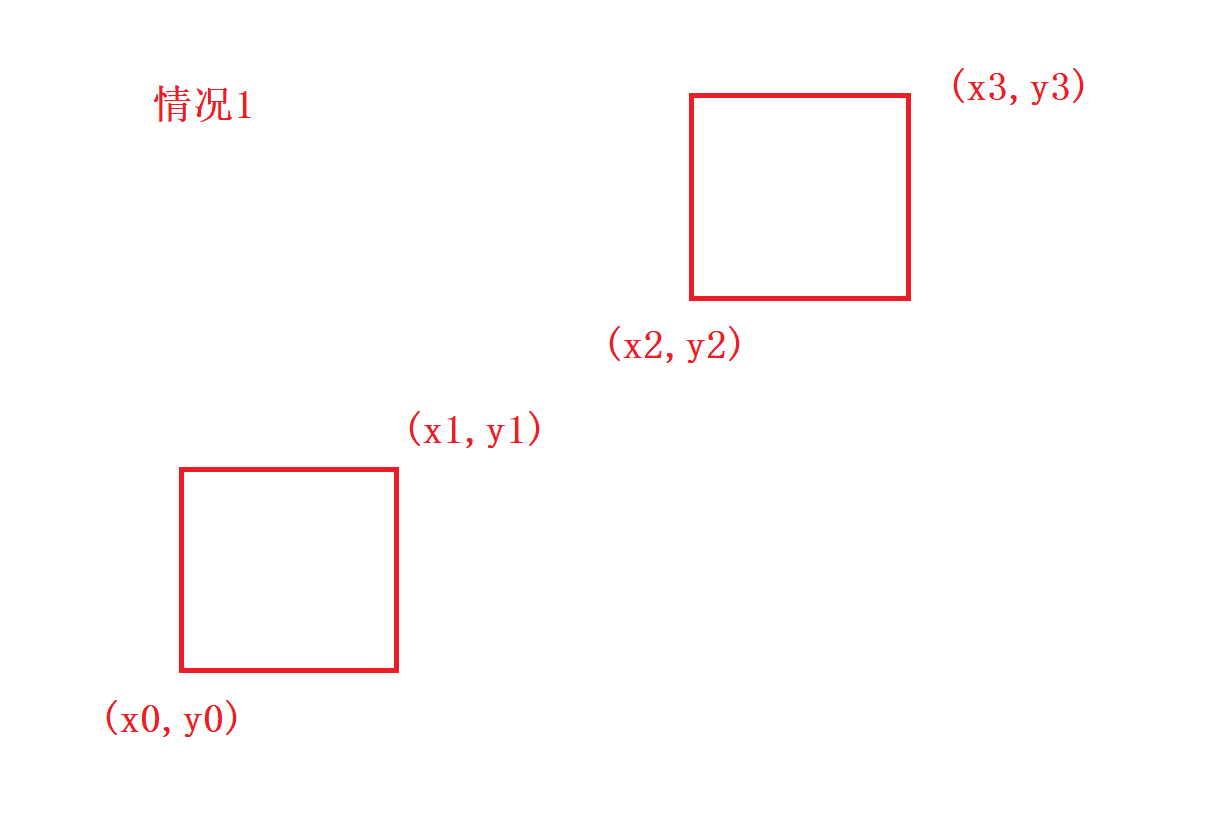
当x[0] >= x[3] || x[1] <= x[2] || y[0] >= y[3] || y[1] <= y[2]表示两个方体一定没有相交

情况二：
当不满足情况一时
Arrays.sort(x,0,4);
Arrays.sort(y,0,4);
无论两个方体怎么相交，相交的区域的左下角一定是(x1,y1)，右上角一定是(x2,y2)

时间复杂度$O(1)$

Java 代码

class Solution {
    public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
        int[] x = new int[4];
        int[] y = new int[4];
        x[0] = A; y[0] = B;
        x[1] = C; y[1] = D;
        x[2] = E; y[2] = F;
        x[3] = G; y[3] = H;
        int sum = (x[1] - x[0]) * (y[1] - y[0]) + (x[3] - x[2]) * (y[3] - y[2]);
        if(x[0] >= x[3] || x[1] <= x[2] || y[0] >= y[3] || y[1] <= y[2])
            return sum;
        else
        {
            Arrays.sort(x,0,4);
            Arrays.sort(y,0,4);
            int t = (x[1] - x[2]) * (y[1] - y[2]);//重叠的面积
            return sum - t;
        }
    }
}