今天做的这个题感觉思维难度不大但是细节调了很久贴下代码记录下来
题目描述
“Help Jimmy” 是在下图所示的场景上完成的游戏。
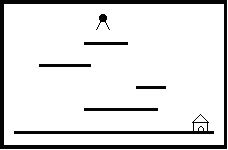
场景中包括多个长度和高度各不相同的平台。地面是最低的平台,高度为零,长度无限。
Jimmy老鼠在时刻0从高于所有平台的某处开始下落,它的下落速度始终为1米/秒。当Jimmy落到某个平台上时,游戏者选择让它向左还是向右跑,它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时,开始继续下落。Jimmy每次下落的高度不能超过MAX米,不然就会摔死,游戏也会结束。
设计一个程序,计算Jimmy到底地面时可能的最早时间。
输入格式
第一行是测试数据的组数t($0 \leq t \leq 20$)。每组测试数据的第一行是四个整数$N,X,Y,MAX$,用空格分隔。$N$是平台的数目(不包括地面),$X$和$Y$是Jimmy开始下落的位置的横竖坐标,$MAX$是一次下落的最大高度。接下来的$N$行每行描述一个平台,包括三个整数,$X1_i$,$X2_i$和$H_i$。$H_i$表示平台的高度,$X1_i$和X2_i表示平台左右端点的横坐标。$1 \leq N \leq 1000$,$-20000 \leq X, X_i, X2_i \leq 20000$,$0 < H_i < Y \leq 20000(i = 1..N)$。所有坐标的单位都是米。
Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘,被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。
输出格式
对输入的每组测试数据,输出一个整数,Jimmy到底地面时可能的最早时间。
题目分析
先对所有有效平台按高度逆序排列考虑设计dp
状态表示:①集合:f[i][0]表示到达第i个平台的左端点,f[i][1]表示到达第i个平台的右端点。②属性:最小值
状态计算:$j->i$
$f[i][0]=min(f[j][1]+a[j].r-a[i].l,f[j][0]+a[j].l-a[i].l)+a[j].h-a[i].h$
$f[i][1]=min(f[j][1]+a[i].r-a[j].r,f[j][0]+a[i].r-a[j].l)+a[j].h-a[i].h$
为保证$j->i$首先可以预处理每个平台从平台两端下落能过到达哪些平台
从一个平台的一端下落到达的平台唯一
代码
//O(n^2)
#define IO ios::sync_with_stdio(false);cin.tie();cout.tie(0)
#pragma GCC optimize(2)
#include<string>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
struct node
{
int l,r,h;
bool operator<(const node &o)const
{
return h>o.h;
}
node(){}
node(int l,int r,int h):l(l),r(r),h(h){}
}a[N];
int n,X,Y,m;
int f[N][2];
bool lok[N][N],rok[N][N];
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d%d%d",&n,&X,&Y,&m);
memset(lok,0,sizeof lok);//忘记初始化debug了很久
memset(rok,0,sizeof rok);
int cnt=0;
for(int i=1;i<=n;i++)
{
int l,r,h;
scanf("%d%d%d",&l,&r,&h);
if(h<=Y) a[++cnt]=node(l,r,h);
}
a[0]=node(X,X,Y);
sort(a+1,a+1+cnt);
a[cnt+1]=node(-200010,200010,0);
for(int i=0;i<=cnt;i++)
{
bool ok1=0,ok2=0;
for(int j=i+1;j<=cnt+1;j++)
{
if(a[i].h>m+a[j].h) continue;
if(!ok1)
{
if(a[i].l>=a[j].l&&a[i].l<=a[j].r)
{
ok1=1;
lok[i][j]=1;
}
}
if(!ok2)
{
if(a[i].r>=a[j].l&&a[i].r<=a[j].r)
{
ok2=1;
rok[i][j]=1;
}
}
if(ok1&&ok2) break;
}
}
memset(f,0x3f,sizeof f);
f[0][0]=0,f[0][1]=0;
int res=0x3f3f3f3f;
for(int i=0;i<=cnt;i++)
{
for(int j=0;j<i;j++)
{
if(lok[j][i])
{
f[i][0]=min(f[i][0],f[j][0]+a[j].l-a[i].l+a[j].h-a[i].h);
f[i][1]=min(f[i][1],f[j][0]+a[i].r-a[j].l+a[j].h-a[i].h);
}
if(rok[j][i])
{
f[i][0]=min(f[i][0],f[j][1]+a[j].r-a[i].l+a[j].h-a[i].h);
f[i][1]=min(f[i][1],f[j][1]+a[i].r-a[j].r+a[j].h-a[i].h);
}
}
if(lok[i][cnt+1]) res=min(res,f[i][0]+a[i].h);
if(rok[i][cnt+1]) res=min(res,f[i][1]+a[i].h);
}
printf("%d\n",res);
}
return 0;
}
要加油哦~

