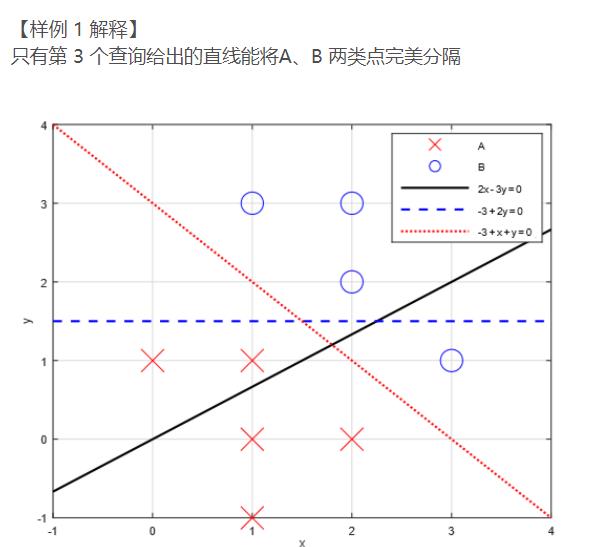
题目描述

考虑一个简单的二分类问题——将二维平面上的点分为A 和B 两类。 训练数据包含 n 个点，其中第 i 个点（1≤i≤n）可以表示为一个三元组 (xi,yi,typei)， 即该点的横坐标、纵坐标和类别。 在二维平面上，任意一条直线可以表示为 θ0 + θ1x+ θ2y = 0 的形式，即由 θ0、θ1 和 θ2 三个参数确定该直线，且满足 θ1、θ2 不同时为 0。 基于这 n 个已知类别的点，我们想要在平面上找到一条直线作为一个线性分类器。 具体来说，这条线要把训练数据中的A、B 两类点 . 完 . 美 . 分 . 隔开来，即一侧只有A 类点、另 一侧只有B 类点。这样，对于任意一个的未知类别的点，我们就可以根据它是位于直线 的哪一侧来预测它的类别了。 在本题中我们仅需要处理 m 个如下查询：给定一条直线，判断它是否能将训练数 据中的A、B 两类点完美分开。

【输入格式】

从标准输入读入数据。 输入共 n + m + 1 行。 第一行包含用空格分隔的两个正整数 n 和 m，分别表示点和查询的个数。 第二行到第 n+1 行依次输入 n 个点的信息。第 i+1 行（1≤i≤n）包含用空格分 隔的三项 xi、yi 和 typei，分别表示第 i 个点的横、纵坐标和类别，其中坐标为整数、类 别为一个大写英文字母A 或B。 第 n + 2 行到第 n + m + 1 行依次输入 m 个查询。第 j + n + 1 行（1≤ j≤m）包含 用空格分隔的三个整数 θ0、θ1 和 θ2，表示第 j 个查询中给定直线的三个参数。

【输出格式】

输出到标准输出。 输出共 m 行，每行输出一个字符串。 第 j 行（1 ≤ j ≤ m）输出的字符串对应第 j 个查询的结果：如果给定直线可以完 美分隔A、B 两类点，则输出Yes；否则输出No。

输入样例

9 3
1 1 A
1 0 A
1 -1 A
2 2 B
2 3 B
0 1 A
3 1 B
1 3 B
2 0 A
0 2 -3
-3 0 2
-3 1 1

输出样例

No
No
Yes

算法

判断两点是否在一条线的同一侧，通常是把这两点坐标同时代入到直线的公式中：o0+o1x+o2y，如果结果相同，则表示在同一侧，如果两个结果不一致，则说明两点在两侧。

判断同类点是否在一侧：1.判断两点是否为同一类
2.如果是同一类判断是否在同一侧

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int x[N];
int y[N];
int cla[N],st[N];
int n,m,o0,o1,o2;
int jdg(int i)
{
    return o0+o1*x[i]+o2*y[i]>0;
}
int main()
{
    cin>>n>>m;
    char c;
    for(int i=0;i<n;i++)
    {
        cin>>x[i]>>y[i]>>c;
        if(c=='A') cla[i]=1;
    }
    while(m--)
    {
        cin>>o0>>o1>>o2;
        for(int i=0;i<n;i++)
        {
            if(jdg(i)) st[i]=1;
            else st[i]=-1;
        }
        int f=0;
        for(int i=0;i<n;i++)
        {
            for(int j=i+1;j<n;j++)
            {
                if(cla[i]==cla[j])
                {
                    if(st[i]!=st[j])
                    {
                        f=1;
                        break;
                    }
                }
            }
            if(f==1) break;
        }
        if(f) cout<<"No"<<endl;
        else cout<<"Yes"<<endl;
    }
    return 0;
}