题目描述

题目：就是给定一个二维数组,然后在给两个坐标(二维数组的下标),(x1,y1),(x2,y2),求第一个坐标的左上角和第二个下标的右下角所组成的范围中存放的数字之和.

输入样例

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例

17
27
21

算法1

(前缀和) $O(n^2)$

**思想**：首先考虑暴力的情况,也就是每次给出两个坐标就遍历一下二维数组求和,那么每次的时间复杂度就是O(n*m),
如果让你求n次,那么时间复杂度就变成了是O(n*m*n),这样就会超时,然后前缀和它就出现了!!!首先前缀和顾名思义就是
求出他的前缀和,假如说我们已经知道了这个数组的前缀和,那么再求小矩阵的时候就可以不用遍历的方式,而是用相减的
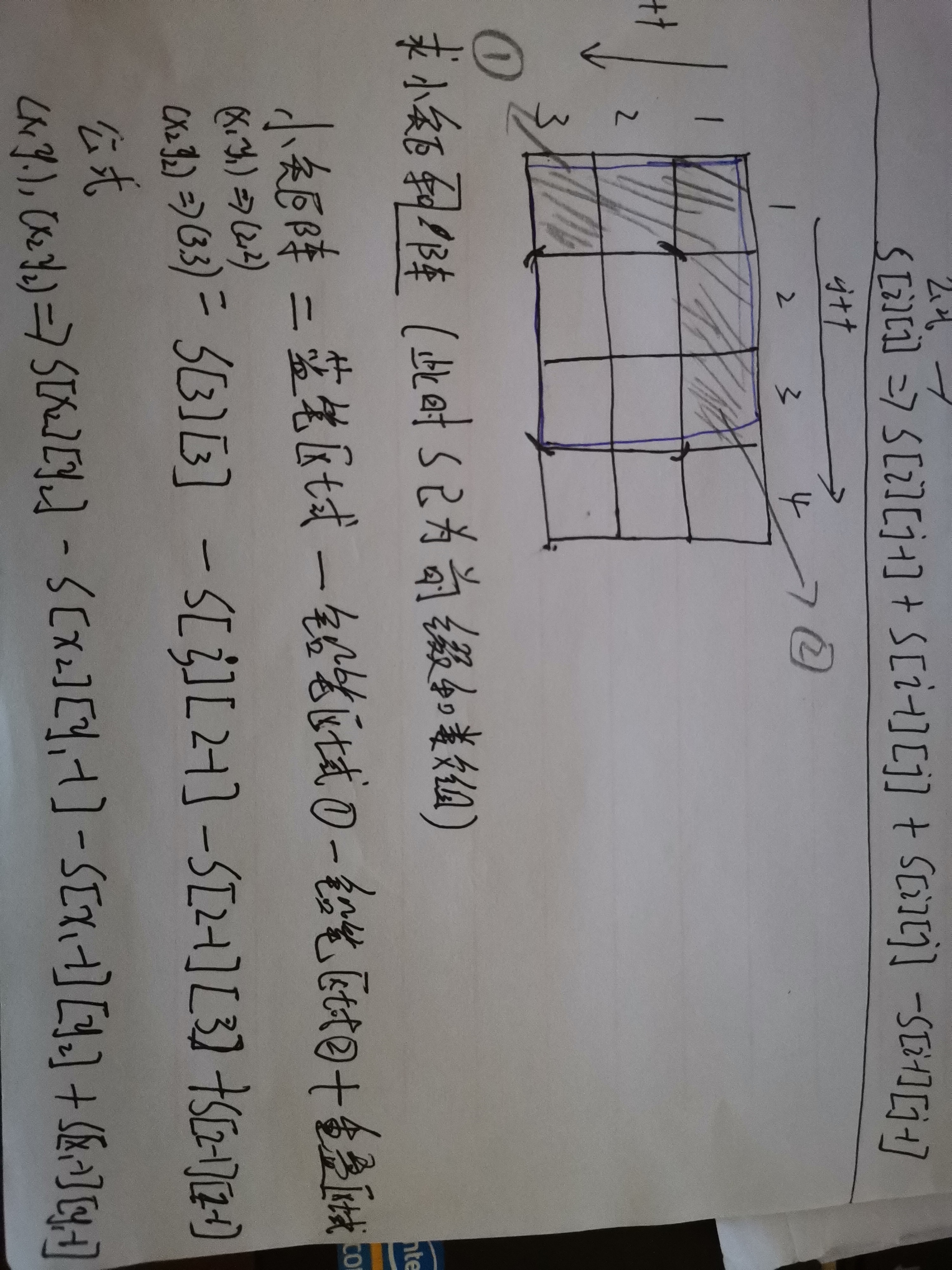
方式,比如：请看下方的第一个图片,这样的话我是用一次加减就求出来了,避免了循环,即上述中的*n.那我们再来考虑一
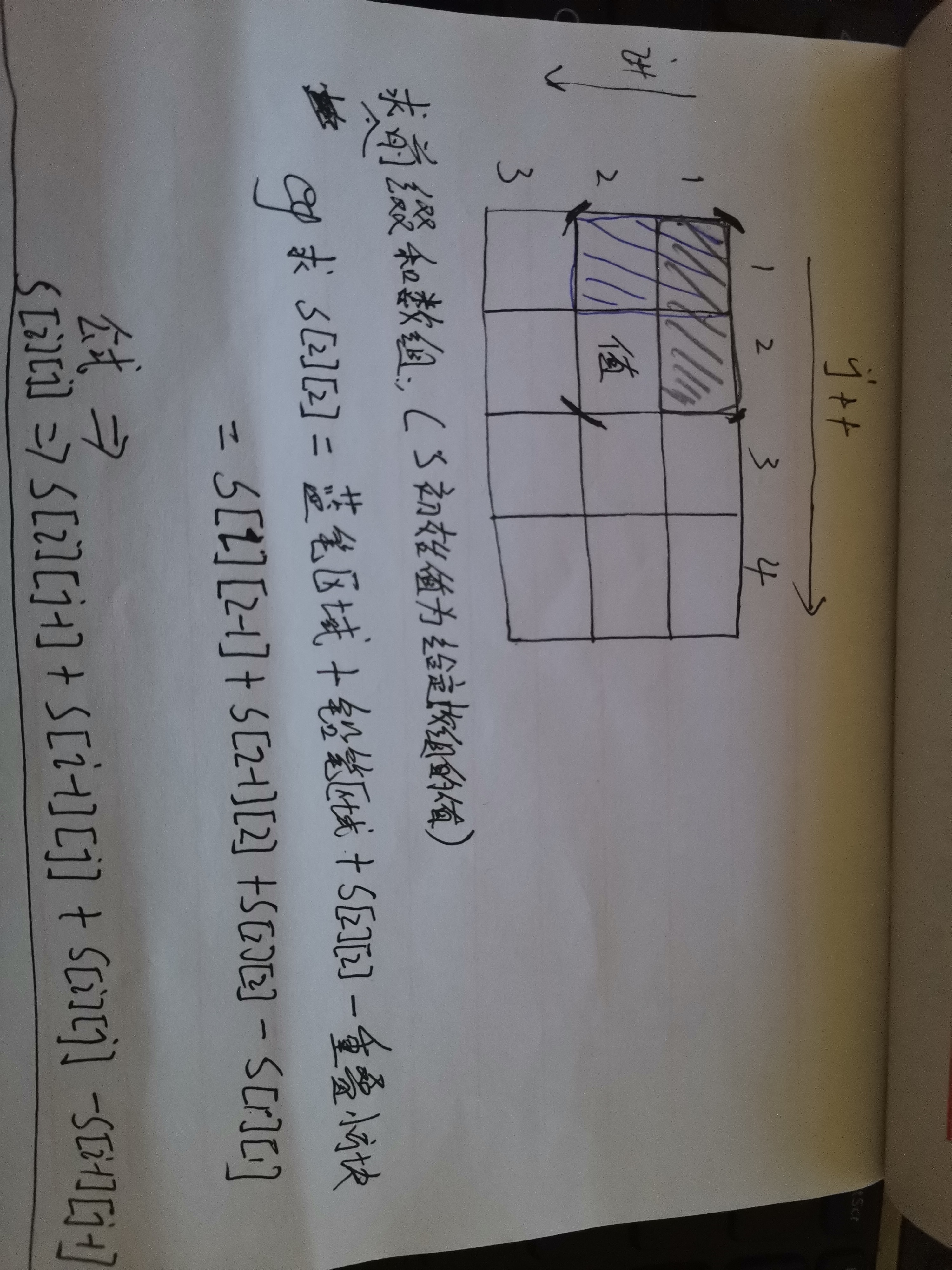
下如何求前缀和数组,请看下方,这样我们求前缀和的时候,不费时间,就是加减,加个循环也就是也就是O(n*n).这样我们
就极大的节省了时间.

求小矩阵的公式

s[i][j] = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]

求前缀和的公式

s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + s[i][j]

时间复杂度：$O(n)$

参考文献：y总

Java 代码

import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main{
    public static final int N = 1010;
    public static int n,m,q;
    public static int[][] s = new int[N][N];

    public static void main(String[] args) throws IOException{
        BufferedReader scan = new BufferedReader(new InputStreamReader(System.in));
        String[] str_01 = scan.readLine().split(" ");
        int n = Integer.parseInt(str_01[0]);
        int m = Integer.parseInt(str_01[1]);
        int q = Integer.parseInt(str_01[2]);

        for (int i = 1; i <= n; i++){
            String[] str_02 = scan.readLine().split(" ");
            for (int j = 1; j <= m; j++) 
                s[i][j] = Integer.parseInt(str_02[j - 1]);
        }

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                s[i][j] += s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1];

        int[] res = new int[q + 1];   
        for (int i = 1; i <= q; i++){
            String[] str_03 = scan.readLine().split(" ");
            int x1 = Integer.parseInt(str_03[0]); int y1 = Integer.parseInt(str_03[1]);
            int x2 = Integer.parseInt(str_03[2]); int y2 = Integer.parseInt(str_03[3]);
            res[i] = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 -1][y1 - 1];
        }

        for (int i = 1; i <= q; i++) System.out.println(res[i]);
    } 
}