#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 100010, M = 400010, mod = 100003;

int n, m;
int head[N], e[M], ne[M], idx;
int dist[N], cnt[N];  // cnt[i],从1到达i的最短路径的条数
int q[N];

void add(int a, int b) {
    e[idx] = b;
    ne[idx] = head[a];
    head[a] = idx ++;
}

// 不能存在长度为0的环
void bfs() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    cnt[1] = 1;

    int hh = 0, tt = 0;
    q[0] = 1; 

    while (hh <= tt) {
        int t = q[hh ++];

        // 记录一下这个点被更新时,更新他的前驱,可以得到一棵树,树是具有拓扑序的
        // 规定一个点只能被一个前驱更新(如果有多个最短路一样的前驱更新他,也认为只有一个)
        for (int i = head[t]; i != -1; i = ne[i]) {
            int j = e[i];  // 枚举t的所有临边(t可以更新到的点)
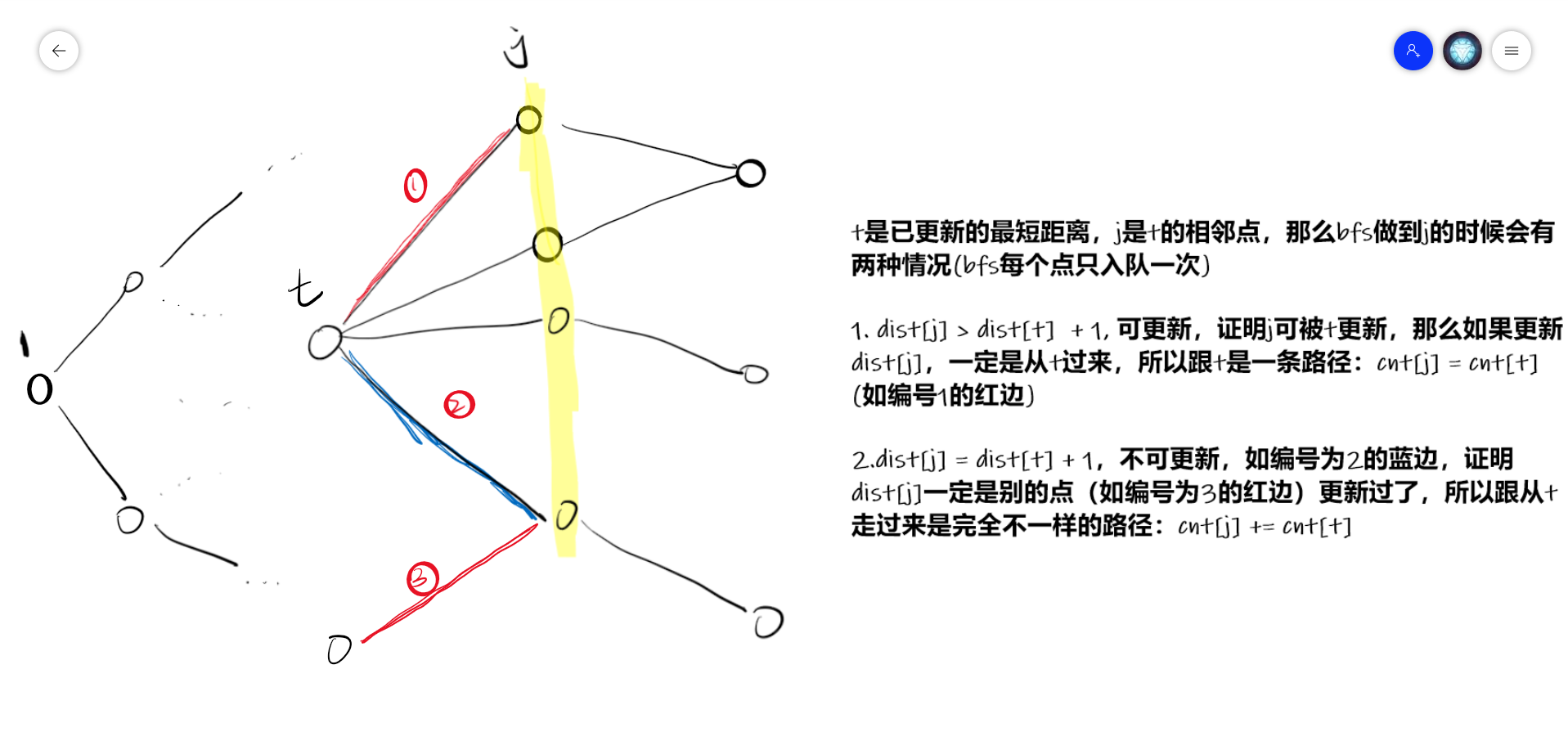
            if (dist[j] > dist[t] + 1) {
                dist[j] = dist[t] + 1;  // 如果用t来更新j,那t一定已经求得最小值
                cnt[j] = cnt[t];  // 如果更新了这条路径的话, 那就跟t是同一条路
                q[++ tt] = j;  // 每个点只入队一次
            }else if (dist[j] == dist[t] + 1)  
                cnt[j] = (cnt[j] + cnt[t]) % mod;
        }
    }
}

int main() {
    cin >> n >> m;
    memset(head, -1, sizeof head);

    while (m --){
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }

    bfs();

    for (int i = 1; i <= n; i ++) cout << cnt[i] << endl;

    return 0;
}