题目描述

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

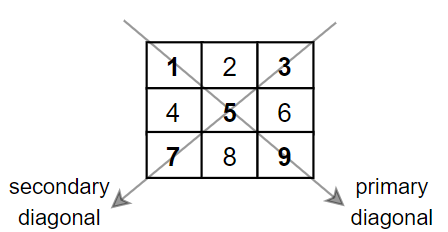
请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

样例

输入：mat = [[1,2,3],
            [4,5,6],
            [7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

输入：mat = [[1,1,1,1],
            [1,1,1,1],
            [1,1,1,1],
            [1,1,1,1]]
输出：8

输入：mat = [[5]]
输出：5

限制

• n == mat.length == mat[i].length
• 1 <= n <= 100
• 1 <= mat[i][j] <= 100

算法

(模拟) $O(n)$

1. 按照题目描述求和。
2. 注意当边长为奇数时，中间的元素只算一次。

时间复杂度

• 对角线的元素共有 $O(n)$ 个，故时间复杂度为 $O(n)$。

空间复杂度

• 仅需要常数的额外空间。

Go 代码

func diagonalSum(mat [][]int) int {
    n := len(mat)

    var ans int
    for i := 0; i < n; i++ {
        ans += mat[i][i] + mat[i][n-i-1]
    }

    if n%2 == 1 {
        return ans - mat[n/2][n/2]
    }

    return ans
}