树的重心（树和图的优先遍历）

思路： 1.求当前节点子树所在块的最大数量
        2. 求当前节点父节点所在块的最大数量
        3.从根节点开始依次以子节点作为重心，使得最大数量是最小的（满足重心要求），则当前的节点就是重心
        4.输出当前节点的子树中的最大节点数量

$\cal{u}$：当前根
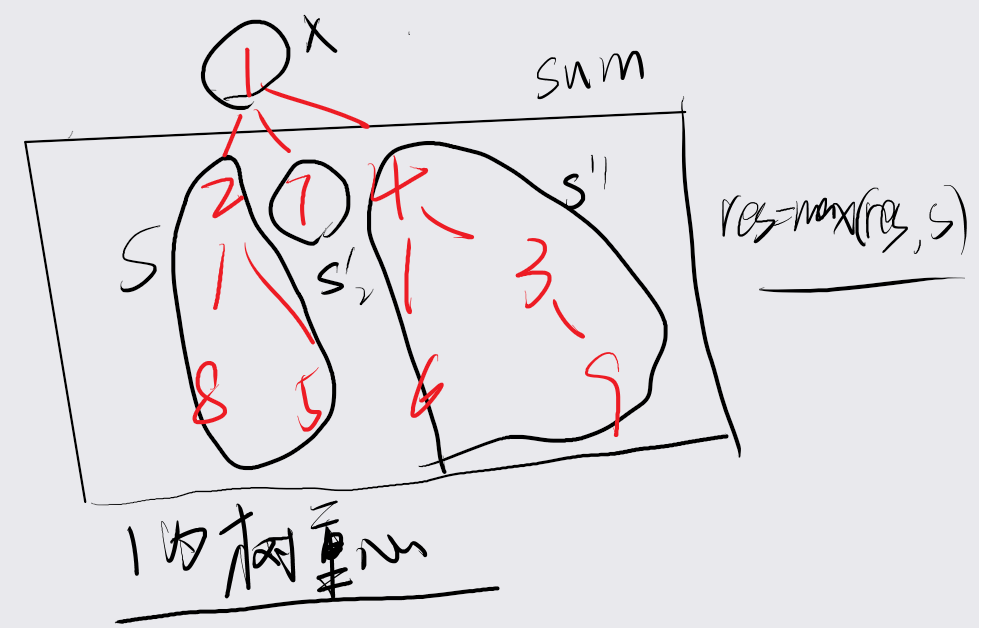
$\cal{res}$：把当前点删掉之后其余块的节点数的最大值
$\cal{Sum}$:当前节点所在块（u）的大小
$\cal{s}$：当前子树（j）的大小
$\cal{Ans}$:最后答案
$\cal{S = dfs(j)}$;//当前子树的大小
$\cal{Res = max(res, s)}$
$\cal{Sum += s}$;//以儿子为根节点的子树是以u为根节点的子树的一部分,因此当前块的大小要加上子树的大小

样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

树和图的优先遍历

$O(n + m)$

时间复杂度

参考文献

y总代码

C++ 代码

#include<iostream>
#include<cstring>
#include<limits.h>
using namespace std;
/*无向边，因此要存两倍的边值*/
const int N = 100010, M = 2 * N;
int h[N], n[M], ne[M], idx, total;
bool st[N];
int ans = INT_MAX;

void add(int a, int b)
{
    n[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

/*u代表当前的节点*/
/*固定模板*/
int dfs(int u)
{

    st[u] = true;
    int sum = 1, res = 0;
    /*当前节点的出度节点*/
    for(int i = h[u]; i != -1; i  = ne[i])
    {
        /*j是当前的点的出度节点（子节点）*/
        int j = n[i];
        /*出度节点没有遍历过*/
        if(!st[j])
        {
            /*求当前节点子树所在块的数量*/
            /*每一次向下递归的时候都把临界点作为了重心*/
            int s = dfs(j);
            /*1.求当前节点子树所在块的最大数量*/
            res = max(res, s);
            sum += s;
        }
    }
   // cout << u << " " << res << endl;
    /*2.求当前节点父节点所在块的最大数量*/
    res = max(res, total - sum);
    /*3.不同节点作为重心的时候，使得其余块的最大数量是最小的（满足重心要求），则当前的节点就是重心*/
    ans = min(ans, res);
    //cout << ans << endl;
    /*返回当前块的大小，当这个点没有出度的时候，返回1*/
    return sum;
}

int main()
{
    memset(h, -1, sizeof(h));
    int a, b;  cin >> total;
    for(int i= 0; i < total - 1; ++i)
    {
         cin >> a >> b;
         /*由于已经有出度和入度的概念，因此是有向图*/
         add(a, b); add(b, a);
    }
    /*假设1为重心，*/
    dfs(1);
    /* 4.输出当前节点的子树中的最大节点数量*/
    cout << ans << endl;
    return 0;
}