n-皇后问题（八皇后）

作为一道经典的题目，那必然要用经典的dfs来做
dfs：深度优先搜索————纵向搜索符合条件的内容，走到底时回到上一个路口再走到底再回去，套娃至结束。

条件：任意一个皇后所在位置的四条线（横、纵、对角、副对角）不能放置其他皇后
横：x
纵：y
副对角：y = x
主对角：y = - x

思路：
平面坐标系中的副对角线实际上也就是二维数组中的主对角线
所以得出:
任意一条副对角线公式为
y = x + b => b = y - x + n(数组中没有负数所以平移n位)
任意一条主对角线公式为
y = - x + b => b = x + y

b 是任意一条主副对角线到（0，0）的截距

那我们就可以通过一个一维数组来表示二维数组中的每一条主副对角线

至多会有2*n条主或副对角线，所以只需要开2n的空间就可以了

下面图随便看看

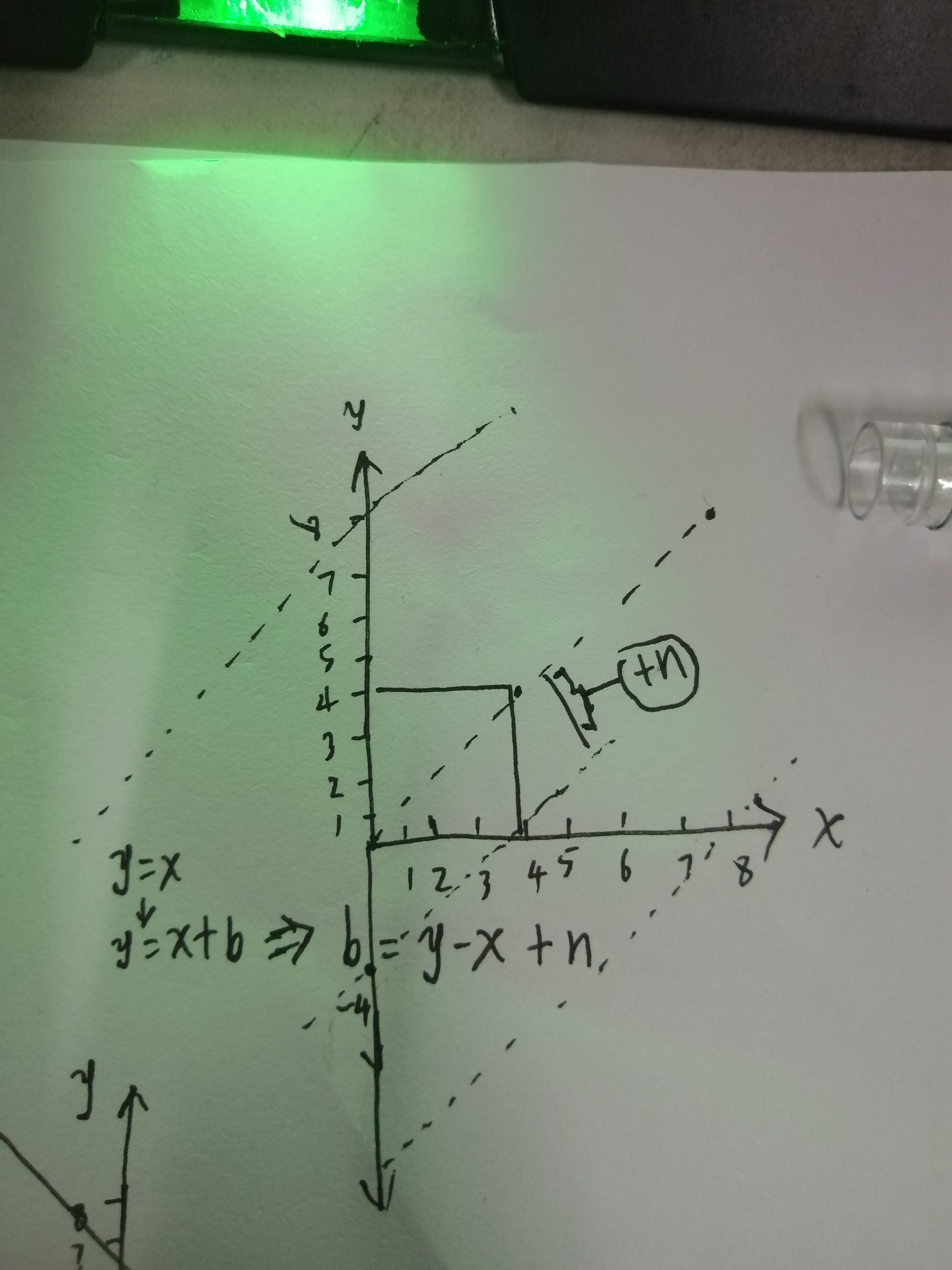
代码奉上

import java.util.*;

public class Main{
    static int n = 0;
    static String[][] path = new String[10][10];
    static boolean[] col = new boolean[20];
    static boolean[] dg = new boolean[20];
    static boolean[] udg = new boolean[20];
    public static void main(String[] args){
        Scanner read = new Scanner(System.in);
        n = read.nextInt();
        for(int i = 0;i < n;i++){
                for(int j = 0;j < n;j++){
                    path[i][j] = ".";
                }
            }
        dfs(0);
    }
    public static void dfs(int k){
        if(k == n){
            for(int i = 0;i < n;i++){
                for(int j = 0;j < n;j++){
                    System.out.print(path[i][j]);
                }
                System.out.println();
            }
            System.out.println();
            return;
        }

         for(int i = 0;i < n;i++){
        if(!col[i] && !dg[k+i] && !udg[i-k+n]){
            path[k][i] = "Q";
            col[i] = dg[k+i] = udg[i-k+n] = true;
            dfs(k+1);
            path[k][i] = ".";
            col[i] = dg[k+i] = udg[i-k+n] = false;
        }
    }
    }

}

时间复杂度