MOD = 100003

def pow_mod(a, k, p):
    t = []
    pow_val = 1             # 2的次幂数, 初始是2^0 = 1
    a_pow = a % p           # a^(2 ^ i)的数值, 初始是a^(2^0) = a
    while pow_val <= k:
        t.append(a_pow)
        a_pow = (a_pow*a_pow) % p
        pow_val <<= 1

    ans = 1
    for i in range(len(t)):
        if k & 1:
            ans = (ans * t[i]) % p
        k >>= 1
    return ans


max_val = 2000
t = [(0, 0)] * (max_val+1)
val = 1
for i in range(1, max_val+1):
    val *= i
    val %= MOD
    _val = pow_mod(val, MOD-2, MOD)     # val的阶乘的逆元
    t[i] = (val, _val)
t[0] = t[1]     # 0! 和 1! 数值是一样的把数值补齐


# a对b的组合数对MOD取模的数值
def C(a, b):
    return (t[a][0] * t[b][1] * t[a-b][1]) % MOD

# a对b排列数对MOD取模的数值
def A(a, b):
    return (t[a][0] * t[a-b][1]) % MOD


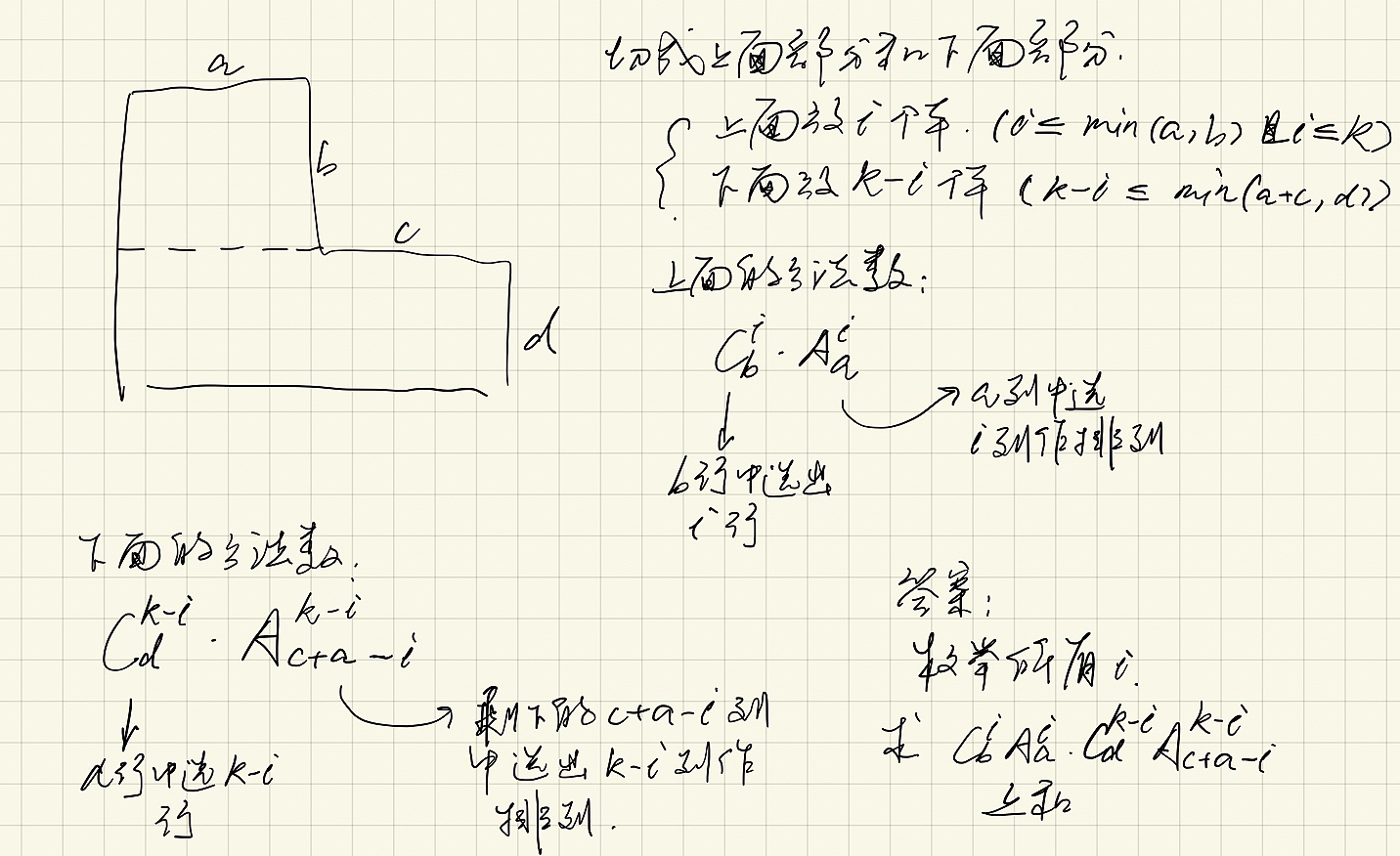
a, b, c, d, k = map(int, input().split())
ans = 0
for i in range(k+1):
    if i <= min(a, b) and (k-i) <= min(a+c, d):
        ans += C(b, i) * A(a, i) * C(d, k-i) * A(a+c-i, k-i)
        ans %= MOD
print(ans)