题目描述
分析:
Prim 和dijkstra 的区别:
Dijkstra
集合:当前以确定的最短距离的点
1.迭代n - 1次,每次寻找不在集合中并且距离最小的节点。
2.找到后放入集合。
3.更新其他节点到起点最短距离。
Prim
集合:当前的生成树(已经在连通块中所有点)
1.迭代n次,每次迭代找到集合外距离最近的点(一开始没有选中一个点,因此迭代n次)。
2.用t更新其他点到**集合**的距离(dijkstra 算法是更新其他点到到**起点**的距离)。
3.更新到集合中。
模拟:
相当于:不是要求到一个点的距离,而是包含所有的点的边的距离最小值。
比如:下面的模拟中,最小值就是,3 到1的最小值 + 4 到(1,3)的最小值 + 2到(1,3, 4)的最小值(每次求的都是当前集合中的点到其他点的最小值,最后肯定是相互之间距离最小的)。
模拟:
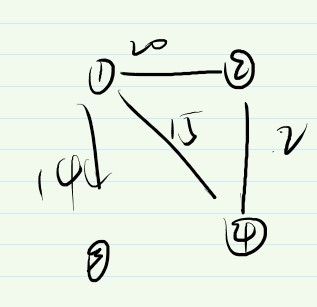
P.S:
问:当前的dist[i] 一定是最小的吗?
一定是到集合中的距离最小的。加上之后再把这个点加入集合中,最后求出来的就是集合中相互距离最小的。
算法1
(暴力枚举) $O(n^2)$
blablabla
时间复杂度
参考文献
C++ 代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 520, INF = 0x3f3f3f3f;
int dist[N],g[N][N], n;
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;dist[1] = 0;
/*重复n次找n个点*/
for(int i = 0; i < n; ++i)
{
/*不确定当前点*/
int t = -1;
for(int j = 1; j <= n; ++j)
{
if(!st[j] && (t == -1 || dist[t] > dist[j]))
{
t = j;
}
}
/*相互之间距离无穷大,说明上一点不能和其他的点联系起来*/
if(dist[t] == INF)return INF;
//cout << t << " " << dist[t] <<endl;
st[t] = true;
/*每次都加上集合中的点到其余点的最小距离*/
/*当前的dist[i] 一定是最小的吗?*/
res += dist[t];
for(int j = 1; j <= n; ++j)
{
/*此时t已经加入到了集合中,因此,g[t][j]表示j到集合中的最短距离*/
//cout << t << " " << j << " "<< g[t][j] <<endl;
dist[j] = min(dist[j], g[t][j]);
//cout << dist[j] <<endl;
}
}
return res;
}
int main()
{
memset(g, 0x3f, sizeof g);
int m, a, b, c;
cin >> n >> m;
while(m--)
{
cin >> a >> b >> c;
/*无向边是特殊的有向边,只需要出边和入边保持一致即可*/
g[a][b] = g[b][a] = min(c, g[a][b]);
}
int ans = prim();
if(ans == INF)puts("impossible");
else cout << ans << endl;
return 0;
}

