题目描述

步骤：
循环系数矩阵的每列：
1.找到绝对值最大的一行
2.将改行放到最上面
3.将该行的第一个数置1
4.把该列下面的数置0
5.循环完后，把每行除了第一个数和最后一个数，其余数置0

易错点：

1.执行步骤4时，要注意a[i][j] -= a[r][j] * a[i][c]
2.执行步骤4时，注意for(int j = n; j >= 0; j–) 要从后往前（因为每次都会用到第c列的值），否则会用到第一个修改的值
2.执行步骤3时，注意for(int j = n; j >= 0; j–) 要从后往前（因为每次都会用到第c列的值），否则会用到第一个修改的值
4.出现了nan, inf 可能出现了以下几种情况：

        1、对负数开方，如：−1.0‾‾‾‾‾√;
        2、对负数求对数，如：log(−1.0)；
        3、0.0 / 0.0；
        4、0.0 * inf；
        5、inf / inf；
        6、nf-inf这些操作都会得到nan。

发现：置1操作的时候从后往前应该截至到c列,否则会除到0
5.注意const double mm = 1e-6 设置成double 不是int， 不然跟没设置一样

样例

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

样例流程图：(红字部分是步骤5)

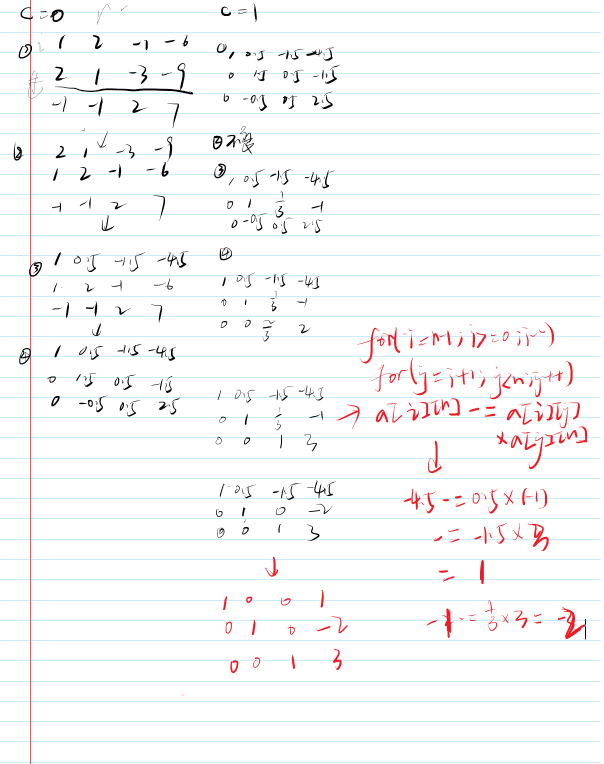
算法1

$O(n^2)$

时间复杂度

参考文献

C++ 代码

#include<iostream>
#include<math.h>
using namespace std;
const int N = 110;
int n;
const double mm = 1e-6;
void gauss(double a[][N])
{
    int r, c;
    for(c = 0, r = 0; c < n; ++c)
    {
        /*1.去绝对值最大的一行*/
        int t = r;
        for(int i = r; i < n; ++i)
        {
            if(fabs(a[t][c]) < fabs(a[i][c]))
            {
                t = i;
            }
        }
        /*如果出现一列都是0的情况，最后结果肯定会出现一行全0的情况*/
        if(fabs(a[t][c]) < mm)continue;
        /*2.交换两行*/
        if(t != r)
            for(int j = 0; j <= n; ++j)
                swap(a[t][j], a[r][j]);
        /*3.把该行第一个数置1*/
       // if(fabs(a[r][c]) > mm)
        for(int j = n; j >= c; j--)
            a[r][j] /= a[r][c];
        /*4.将下面所有行的第c列清空成0*/
        for(int i = r + 1; i < n; ++i)
        {
            if(fabs(a[i][c]) > mm)
            for(int j = n; j >= c; j--)
            {
                a[i][j] -= a[r][j] * a[i][c];
            }
        }
/*                for(int i = 0; i < n; ++i)
        {
            for(int j = 0; j <= n; ++j)
                printf("%5.2f ", a[i][j]);
            puts(""); 
        }*/
        r++;
    }

    //cout << r << endl;
    if(r < n)
    {
        bool has_so = false;
        for(int i = 0; i < n; ++i)
            if(fabs(a[i][n]) < mm)
                has_so = true;    
        if(has_so)
            puts("Infinite group solutions"); 
        else 
            puts("No solution");
    }
    else
    {
    /*最后让其余不没行最左边的数置0*/
    /*为什么要从后往前呢？怎么思考的？*/
    /*因为正常解非齐次线性方程的时候就是从下到上把数置0，当后面的列都只有1个数的时候更适合计算前面行*/
    for(int i = n - 1; i >= 0; i--)
        for(int j = i + 1; j < n; ++j)
            {
                a[i][n] -= a[i][j] * a[j][n];
            }
        for(int j = 0; j < n; ++j)
            printf("%.2lf\n", a[j][n]);
    }
}


int main()
{
    cin >> n;double a[N][N];
    for(int i = 0; i < n; ++i)
    {
        for(int j = 0; j <= n; ++j)
            cin >> a[i][j];
    }
    gauss(a);


    return 0;
}