/*
         o
        / \
       o   o
      / \
     o   .
    / \
   .   o
         o
        / \
       .   o
      / \
     o   .
    / \
   .   o
方法1 向上标记法 O(n)
          o
        ↗ \
       .    o
     ↗ \
     o   .
   ↗ \   2
  .   o
  1
步骤
1 先从点1往上走到根节点,走过的点都标记
2 再从点2往上走,碰到的第一个带标记的点就是最近公共祖先

方法2 倍增法 预处理(nlogn) + 查询(logn)
 ⭐关键是理解二进制拼凑  在这里是怎么体现的
  即 x,y从同一高度同时起跳后,在f[x][0]!=f[y][0] 的约束下 我们能跳的最多的步数跳完后 x,y就达到了LCA的下面一层 
  假定我们知道 x,y出发点为第1层 
               LCA下一层为第12层
那么最多能跳的步数t = 12-1 = 11 = (1011)2 = 最多能跳2^3 + 2^2 + 2^0 步
 所以我们就通过从大到小枚举k使得我们刚好跳11步而不能跳超过12步
 但实际上我们并不知道要跳11步,所以我们可以通过f[x][0]!=f[y][0]的约束来实现
 即f[x][总共>=12步] = f[y][总共>=12步] 那就不跳(不拼凑2^k)
   f[x][总共<12步] != f[y][总共<12步] 那就跳(拼凑2^k)

预处理出每个点向上走2^k步的节点的父亲是谁
f[i][j] 从i开始向上走2^j步所能走到的节点 0<=j<=logn
         1
        / \
       2   3
      / \
     4   5
    / \
   6   7
 f[6][0] = 4
 f[6][1] = 2
 f[6][2] = 空集
j=0 f[i][j] = i的父节点
j>0 f[i][j-1]
i  →  mid  →  t
  2^j-1  2^j-1
  f[i][j-1] f[i][j]
mid = f[i][j-1]  
t = f[i][j]
则f[i][j] = f[mid][j-1] = f[f[i][j-1]][j-1]
depth[i]表示深度/层数
         1
        / \
       2   y
      / \
     4   5
    / \
   x   7

步骤1  把两个点跳到同一层 把x跳到和y同一层

二进制拼凑 2^0 ~ 2^k   t
     举例  2^0 ~ 2^4   11                
          1 2 4 8 16   11              二进制
                       16>11              0
                       8<11 t = 11-8 = 3  1
                       4>3                0
                       2<3  t = 3-2 = 1   1
                       1>=1       t = 1   1
    二进制 (1011)2
    depth(x) - depth(y)
从x跳到y
从x跳2^k步后的点的深度 depth(f[x][k]) >= depth(y)时 就可以继续跳

步骤2 在depth(x)==depth(y)后  一起往上跳2^k(for k in [log(n),1]
情况1 x==y 则该点就是x和y的最近公共祖先
情况2 x!=y 即他俩同层但不同
           则继续让两个点同时往上跳 一直跳到它们的最近公共祖先的下一层
             1        1
            / \      / \
           2   y    x   y
          / \      / \
         4   5    4   5
        / \      / \
       x   7    6   7
           why 最近公共祖先的下一层 not 最近公共祖先？
           方便判断
           假如f[x][k] == f[y][k] <=> f[x][k] or f[y][k]是x和y的一个公共祖先 但不一定是最近的
           举个栗子
           此时f[x][1] == f[y][1] = 节点2 是x和y的一个公共祖先 但不是最近公共祖先4
           ,但由于我们是从大到小拼凑的,假如拼凑终止条件为f[x][k] == f[y][k]
           ,则此时会停在公共祖先2而非最近公共祖先4
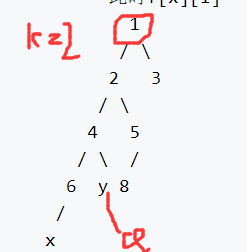
             1        
            / \      
           2   3    
          / \      
         4   5   
        / \  /   
       x  y 8

     步骤一 x先到y同一层 f[x][0]!=f[x][0] 且把k能填1的都填完了

   加上约束 f[x][k] != f[y][k]
   思考一下为啥: 因为第一个出现f[x][k] == f[y][k]的节点只是公共祖先却不能保证是最近公共祖先
   所以只要 f[x][k] != f[y][k]
       那么 x y就还没跳到过最近公共祖先,而在其下面层 
   从大往小枚举k
   枚举过程中
       只要 f[x][k] != f[y][k]
       那么 x y就还没跳到过最近公共祖先,而在其下面层,则x,y更新为f[x][k] f[y][k]
 这个过程中 f[x][k] == f[y][k]时
       不执行跳2^k步跳到 f[y][k] 的操作
   直到k枚举完为止 
   枚举完之后就走到了最近公共祖先的下一层
   二进制拼凑 2^0 ~ 2^k   t
     这里的k最大为logn   
     t为 x和y达到同一高度(depth(起始)) - 最近公共祖先下一层深度-1(depth(祖先)-1)

     举例  2^0 ~ 2^4     2                
          1 2 4 8 16     2             二进制
                         16>2               0
                         8>2                0
                         4>2                0
                         2=2  t = 2-2 = 0   1
                         1>0                0
             1        
            / \      
           2   3    
          / \   \   
         4   5   8
        / \       \
       x   7       9
             1      \  
            / \      y
           2   3    
          /  \  \     
         4    5  8
        / \       \
       x  7        y
       在这个例子里 k=4  t=2(4(x,y出发层)-2(LCA下一层))[通过f[x][k] != f[y][k]约束]
             1       
            / \      
           x   y    
          /  \  \     
         4    5  8
        / \       \
       6  7        9
   此时它们的最近公共祖先就是x or y往上跳一步
   即LCA  = f[x][0] or f[y][0]


*/

#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;

const int N = 40010, M = N * 2;

int n, m;
int h[N], e[M], ne[M], idx;
int depth[N], fa[N][16];//往上跳2^k步后的父亲节点
int q[N];

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}

void bfs(int root)//宽搜不容易因为递归层数过多爆栈
{
    memset(depth,0x3f,sizeof depth);
    // 哨兵depth[0] = 0: 如果从i开始跳2^j步会跳过根节点 
    // fa[fa[j][k-1]][k-1] = 0
    // 那么fa[i][j] = 0 depth[fa[i][j]] = depth[0] = 0
    depth[0] = 0,depth[root] = 1;
    queue<int> q;
    q.push(root);
    while(q.size())
    {
        int t = q.front();
        q.pop();
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j = e[i];
            if(depth[j]>depth[t]+1)//说明j还没被搜索过
            {
                depth[j] = depth[t]+1;
                q.push(j);//把第depth[j]层的j加进队列
                fa[j][0] = t;//j往上跳2^0步后就是t
                /*
                i  →  mid  →  t
                  2^j-1  2^j-1
                  f[i][j-1] f[i][j]
                mid = f[i][j-1]  
                t = f[i][j]
                则f[i][j] = f[mid][j-1] = f[f[i][j-1]][j-1]
                */
                for(int k=1;k<=15;k++)
                {
                    fa[j][k] = fa[fa[j][k-1]][k-1];
                }
                /*
                举个例子理解超过根节点是怎么超过的
                因为我们没有对根节点fa[1][0]赋值,那么fa[1][0] = 0;
                    1
                   / \
                  2   3 
                fa[1][0] = 0;
                fa[2][0] = 1;
                fa[2][1] = fa[fa[2][0]][0] = fa[1][0] = 0;
                */
            }
        }
    }
}

int lca(int a, int b)
{
    // 为方便处理 当a在b上面时 把a b 互换  
    if (depth[a] < depth[b]) swap(a, b);
    //把深度更深的a往上跳到b
    for (int k = 15; k >= 0; k -- )
        //当a跳完2^k依然在b下面 我们就一直跳
        //二进制拼凑法
        //这里因为
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
    //如果跳到了b
    if (a == b) return a;
    //a,b同层但不同节点
    for (int k = 15; k >= 0; k -- )
        // 假如a,b都跳出根节点,fa[a][k]==fa[b][k]==0 不符合更新条件
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    //循环结束 到达lca下一层
    //lca(a,b) = 再往上跳1步即可
    return fa[a][0];
}

int main()
{
    cin >> n;
    int root = 0;
    memset(h, -1, sizeof h);

    for (int i = 0; i < n; i ++ )
    {
        int a, b;
        cin >> a >> b;
        if (b == -1) root = a;
        else add(a, b), add(b, a);
    }

    bfs(root);//建fa[i][j]

    scanf("%d", &m);
    while (m -- )
    {
        int a, b;
        cin >> a >> b;
        int p = lca(a, b);
        if (p == a) cout << "1" << endl;
        else if (p == b) cout << "2" << endl;
        else cout << "0" << endl;
    }
    return 0;
}