题目：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问 数列中第 l~r 个数的和。

分析树状数组

1. 修改某一个元素
2. 求前缀和

第一问： 可以用差分的思想，完成题目的”C” 操作的求法。

差分： b1 + b2 + … bn = an
-> b1 = a1 - a0
-> b2 = a2 - a1
…

第二问： 从第一问求的差分， 求第二问的话，ans

    for(int i = 1; i <= x; i++){
        for(int j = 1; j <= i; j++){
            ans += bj  //这里的bj就是差分的元素
        }
    }

二维循环画图分析：

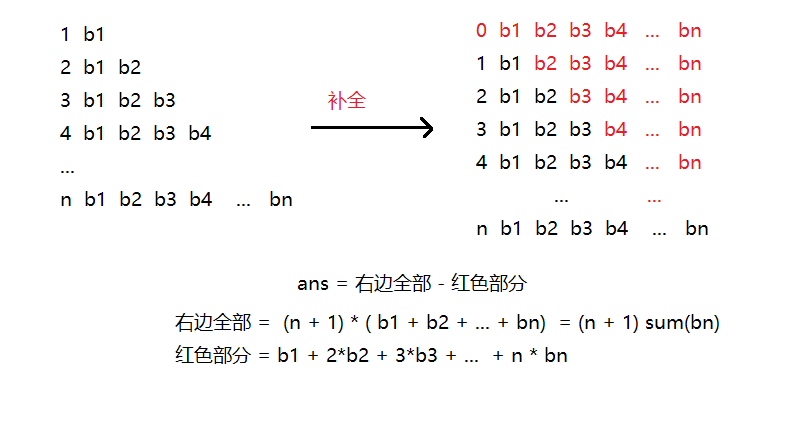
时间复杂度 O(nlogn)

import java.io.*;
class Main{
    static BufferedReader read = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter log  = new BufferedWriter(new OutputStreamWriter(System.out));
    // tr1表示差分树状数组    tr2表示差分*i 树状数组
    static int[] a;
    static long[] tr1, tr2;
    static int n, m;
    public static void main(String[] args) throws Exception{
        String[] ss = read.readLine().split(" ");
        n = Integer.valueOf(ss[0]); m = Integer.valueOf(ss[1]);
        a = new int[n + 1]; tr1 = new long[n + 1]; tr2 = new long[n + 1];
        ss = read.readLine().split(" ");
        for(int i = 1; i <= n; i++){
            a[i] = Integer.valueOf(ss[i - 1]);
            add(tr1, i, (long)a[i] - a[i - 1]);
            add(tr2, i, (long)(a[i] - a[i - 1]) * i);
        }

        while(m --> 0){
            ss = read.readLine().split(" ");
            int l = Integer.valueOf(ss[1]);
            int r = Integer.valueOf(ss[2]);
            switch(ss[0]){
                case "Q":
                    long res = (sum(tr1, r) * (r + 1) - sum(tr2, r)) -
                    (sum(tr1, l - 1) * l - sum(tr2, l - 1));
                    log.write(res + "\n");
                    break;
                case "C":
                    int c = Integer.valueOf(ss[3]);
                    add(tr1, l, c); add(tr1, r + 1, (long)(-c));
                    add(tr2, l, l * c); add(tr2, r + 1, (long)(r + 1) * (-c) );
                    break;
            }
        }
        log.flush();

    }

    public static void add(long[] tr, int x, long c){
        for(int i = x; i <= n; i += lowBit(i)) tr[i] += c;
    }

    public static long sum(long[] tr, int x){
        long res = 0;
        for(int i = x; i > 0; i -= lowBit(i)) res += tr[i];
        return res;
    }
    public static int lowBit(int x){
        return x & - x;
    }
}