有线电视网络

Solution

网络流建模


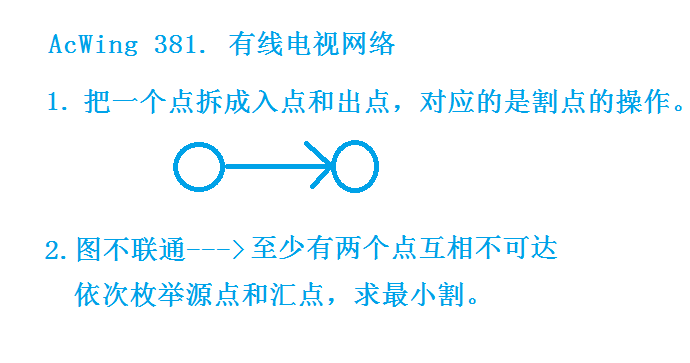
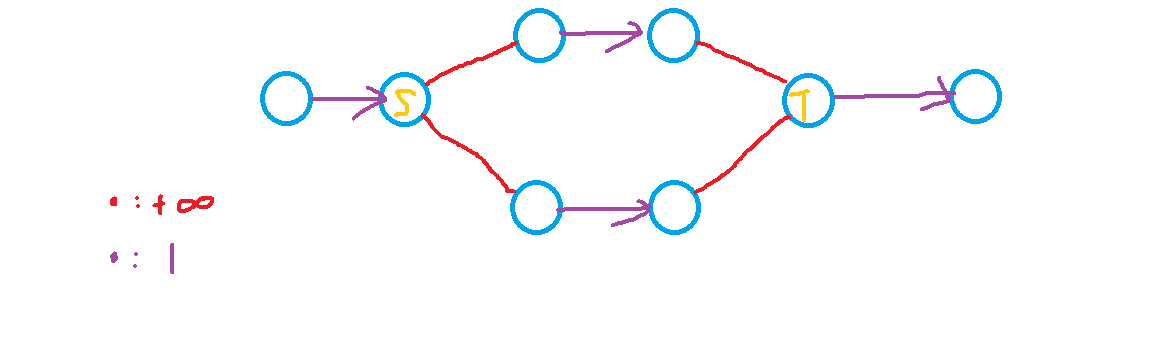
源点枚举的是点的出点，汇点枚举的是点的入点。
但如果仅仅这样的话，我们发现网络流中的最小割与原问题的解不是一一对应的。
这是因为最小割中一定不包括源点和汇点，
但是只要原问题的解最后余下两个点以上，这种方案已经包括在最小割中了。
所以我们分别考虑最后只余下一个点和零个点的情况，

• 一个点的话，图还连通，不符题意。
• 零个点的话，符合题意，需要割掉的点数为n。

ans=min(n,maxflow)

Code

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int N=500,M=1e4+5,INF=1e9+5;
int one[N],idx=1;
int ver[M],Next[M],edge[M],e[M];
inline void AddEdge(int a,int b,int c)
{
    Next[++idx]=one[a];
    one[a]=idx;
    ver[idx]=b;
    e[idx]=c;
//  printf("%d ---> %d\n",a,b);
    return;
}
//============================
int n,m,S,T;
queue<int> q;
int d[N],cur[N];
bool bfs()
{
    memset(d,-1,sizeof d);
    memcpy(cur,one,sizeof cur);
    while(q.size()) q.pop();
    int i,x,y;
    q.push(S); d[S]=1;
    while(q.size()) {
        x=q.front(); q.pop();
        for(i=one[x];i>0;i=Next[i]) {
            y=ver[i];
            if(edge[i] && d[y]==-1) {
                d[y]=d[x]+1;
                if(y==T) return true;
                q.push(y);
            }
        }
    }
    return false;
}
int dinic(int x,int limit)
{
    if(x==T) return limit;
    int i,y,flow=0,k;
    for(i=cur[x];i>0 && flow<limit;i=Next[i]) {
        cur[x]=i;
        y=ver[i];
        if(edge[i] && d[y]==d[x]+1) {
            k=dinic(y,min(edge[i],limit-flow));
            if(k==0) d[y]=-1;
            edge[i]-=k; edge[i^1]+=k;
            flow+=k;
        }
    }
    return flow;
}
int main()
{
//  freopen("1.in","r",stdin);
    int i,x,y;
    int ans,maxflow;
    char c;
    while(scanf("%d%d",&n,&m)==2) {
        memset(one,0,sizeof one);
        memset(ver,0,sizeof ver);
        memset(e,0,sizeof e);
        memset(Next,0,sizeof Next);
        idx=1;

        for(i=1;i<=m;i++) {
            cin>>c;
            scanf("%d,%d",&x,&y);
            cin>>c;
            x++; y++;
            AddEdge(x+n,y,INF);
            AddEdge(y,x+n,0);
            AddEdge(y+n,x,INF);
            AddEdge(x,y+n,0);   
        }
        for(i=1;i<=n;i++) 
            AddEdge(i,i+n,1),AddEdge(i+n,i,0);
        ans=n;
        for(S=n+1;S<=2*n;S++) 
            for(T=S-n+1;T<=n;T++) {
                memcpy(edge,e,sizeof edge);
                maxflow=0;
                while(bfs()) 
                    while((x=dinic(S,INF))) 
                        maxflow+=x;
                ans=min(ans,maxflow);
            }
        printf("%d\n",ans);
    }
    return 0;
}