题目

有n头奶牛，已知它们的身高为 1~n 且各不相同，但不知道每头奶牛的具体身高。

现在这n头奶牛站成一列，已知第i头牛前面有Ai头牛比它低，求每头奶牛的身高。

输入格式
第1行：输入整数n。

第2..n行：每行输入一个整数Ai,第i行表示第i头牛前面有Ai头牛比它低。
（注意：因为第1头牛前面没有牛，所以并没有将它列出）

输出格式
输出包含n行，每行输出一个整数表示牛的身高。

第i行输出第i头牛的身高。

数据范围
1≤n≤105
输入样例：
5
1
2
1
0
输出样例：
2
4
5
3
1

思路

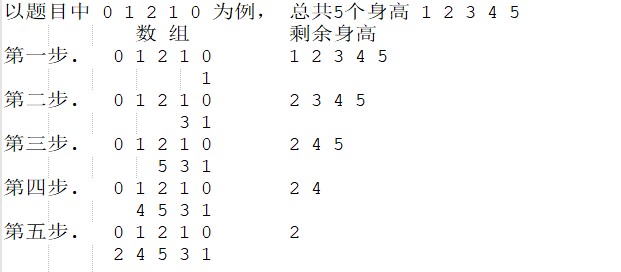
从上面分析可得， 从右向左枚举数组a， 当前牛身高为第a[i] + 1 小的数

所以， 做这个题， 我们需要两种操作：
1. 从剩余的身高里面找到第 k 小的数
2. 删除使用过的身高

方法一：

使用单链表就能实现这个操作了。
时间复杂度O(n ^ 2), 因为单链表的查找操作是O(n), 但是TLE了， 过了9/10测试数据。

方法二：

我们可以把身高作为下标维护到树状数组里面
只要找到最左边的x，使得sum(x) == k， 意思就是： 剩余k个身高小于等于x的数
为什么要找最左边的， 因为最左边的一定是1， 未被使用过的数
此时牛的身高就是x， 并使用add(x, -1), 移除这个使用过的身高

并且， 由于构成的树状数组是调单递增的阶梯状图型， 因此可以加入二分查找进行优化。

时间复杂度 O( n * (logn) ^ 2 )

import java.io.*;
import java.util.*;
class Main{
    static BufferedReader read = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter log  = new BufferedWriter(new OutputStreamWriter(System.out));
    static int[] a, tr, ans;
    static int n;
    public static void main(String[] args) throws Exception{
        n = Integer.valueOf(read.readLine());
        List<Integer> list = new LinkedList();
        a = new int[n + 1];
        tr = new int[n + 1];
        ans = new int[n + 1];
        for(int i = 2; i <= n; i++) a[i] = Integer.valueOf(read.readLine());
        for(int i = 1; i <= n; i++) add(i, 1);
        for(int i = n; i >= 1; i--){
            int k = a[i] + 1;
            int l = 1, r = n;
            while(l < r){
                int mid = l + r >> 1;
                if( sum(mid) >= k ) r = mid;
                else l = mid + 1;
            }
            ans[i] = l;
            add(l, -1);
        }
        for(int i = 1; i <= n; i++) log.write(ans[i] + "\n");
        log.flush();
    }

    public static int lowBit(int x){return x & -x;}

    public static void add(int x, int c){
        for(int i = x; i <= n; i += lowBit(i)){
            tr[i] += c;
        }
    }

    public static int sum(int x){
        int res = 0;
        for(int i = x; i > 0; i -= lowBit(i)) res += tr[i];
        return res;
    }
}