题目描述

秋游中的小力和小扣设计了一个追逐游戏。他们选了秋日市集景区中的 N 个景点，景点编号为 1~N。此外，他们还选择了 N 条小路，满足任意两个景点之间都可以通过小路互相到达，且不存在两条连接景点相同的小路。整个游戏场景可视作一个无向连通图，记作二维数组 edges，数组中以 [a,b] 形式表示景点 a 与景点 b 之间有一条小路连通。

小力和小扣只能沿景点间的小路移动。小力的目标是在最快时间内追到小扣，小扣的目标是尽可能延后被小力追到的时间。游戏开始前，两人分别站在两个不同的景点 startA 和 startB。每一回合，小力先行动，小扣观察到小力的行动后再行动。小力和小扣在每回合可选择以下行动之一：

• 移动至相邻景点
• 留在原地

如果小力追到小扣（即两人于某一时刻出现在同一位置），则游戏结束。若小力可以追到小扣，请返回最少需要多少回合；若小力无法追到小扣，请返回 -1。

注意：小力和小扣一定会采取最优移动策略。

样例

样例一：

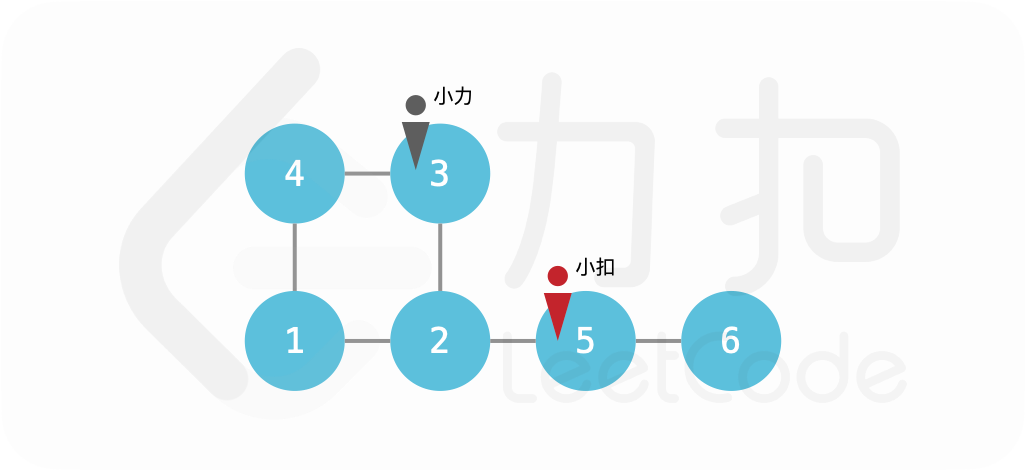
输入：edges = [[1,2],[2,3],[3,4],[4,1],[2,5],[5,6]], startA = 3, startB = 5

输出：3

解释：

第一回合，小力移动至 2 号点，小扣观察到小力的行动后移动至 6 号点；
第二回合，小力移动至 5 号点，小扣无法移动，留在原地；
第三回合，小力移动至 6 号点，小力追到小扣。返回 3。

样例二：

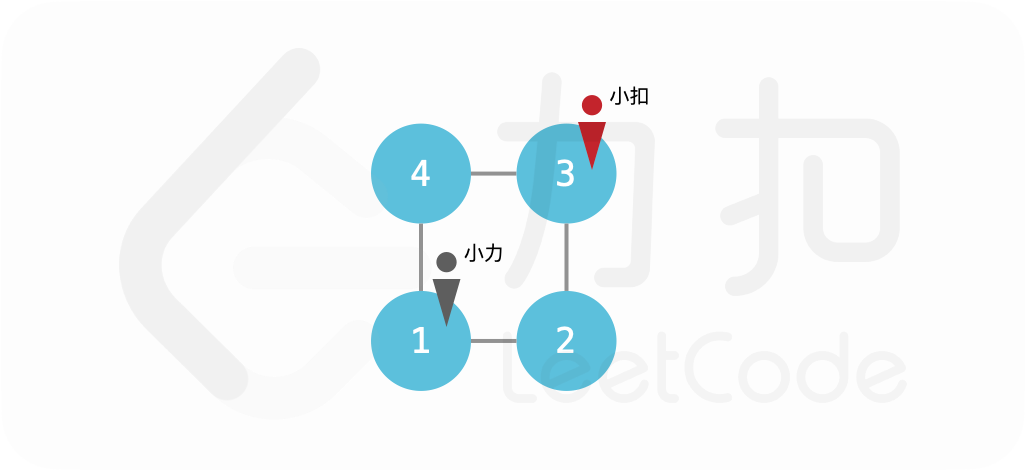
输入：edges = [[1,2],[2,3],[3,4],[4,1]], startA = 1, startB = 3

输出：-1

解释：
小力如果不动，则小扣也不动；否则小扣移动到小力的对角线位置。这样小力无法追到小扣。

提示：

• edges 的长度等于图中节点个数
• 3 <= edges.length <= 10^5
• 1 <= edges[i][0], edges[i][1] <= edges.length 且 edges[i][0] != edges[i][1]
• 1 <= startA, startB <= edges.length 且 startA != startB

算法分析

环上树

题目说到，共有n个景点，编号是1到n，且有n条边，由此可知，该图一定且只存在一个环，由于小力和小扣都选择最优策略，小力一定要最快抓到小扣，小扣一定不让小力抓到或者最晚被他抓到，

分两种情况

• 1、假设环足够大时(n > 3)
  • (1)若小扣在环上，则小力永远追不到小扣
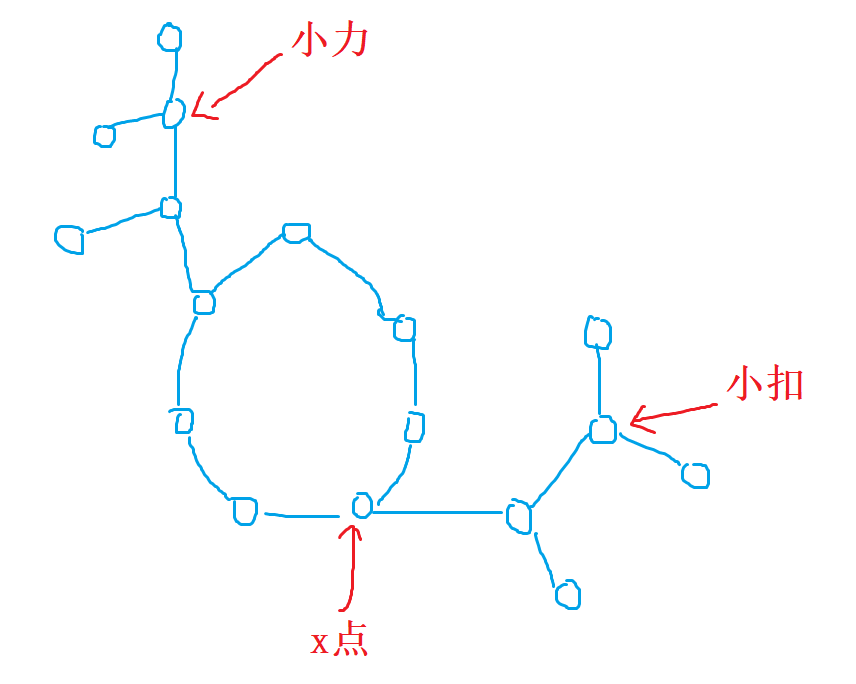
  • (2)若小扣不在环上，而是在环上的某个树分支中，那么小扣若不想被小力追到，则小扣一定要往环方向走，只要在小力追到小扣之前，小扣到达环上即安全，如图所示，只要小扣先于小力到达x点，则小力永远追不到小扣
• 2、假设环的长度刚好等于3，则即使小扣在环上，小力也可以在环上追到，环的某个树分支中也一定会被追到，因此小力一定会追到小扣

其中，当小扣得知小力一定会追到他时，一定会让小力尽可能走更远的路才追到他才是最优策略

具体操作

• 1、跑两遍bfs，分别求出小力到所有点的最短距离distA[] 以及 小扣到所有点的最短距离distB[]
• 2、对图进行拓扑排序找出环的长度res，由于图的边都是双向边，因此开始将所有入度为1的点加入到队列中，进行拓扑排序，最终没有进队列的点一定是入度为2的点，所有入度为2的点会组成的就是要找的环
• 3、判断res的值
  若res == 3，枚举所有点，找到所有小力一定比小扣后到达的点的集合的最大值ans
  若res > 3，枚举所有点
  若能找到某些点，小力一定比小扣后到达，且该点在环上（入度为2），则直接返回-1。否则，找到所有小力一定比小扣后到达的点的集合的最大值ans

注意：小力是先手走的，比较小力和小扣到达某个点比谁早，是用distA[i] 和 distB[i] + 1进行比较

时间复杂度 $O(n)$

参考文献

参考了排名第1的 zerotrac的代码

Java 代码

class Solution {
    static int N = 100010, M = 2 * N;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int idx = 0;
    static int[] distA = new int[N];
    static int[] distB = new int[N];
    static int[] d = new int[N];
    static int INF = 0x3f3f3f3f;
    static int n;
    static void add(int a, int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static void bfs(int[] dist, int start)
    {
        Arrays.fill(dist, -1);
        dist[start] = 0;
        Queue<Integer> q = new LinkedList<Integer>();
        q.add(start);
        while(!q.isEmpty())
        {
            int t = q.poll();
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                if(dist[j] == -1) 
                {
                    dist[j] = dist[t] + 1;
                    q.add(j);
                }
            }
        }
    }
    static int topsort()
    {
        int res = n;
        Queue<Integer> q = new LinkedList<Integer>();
        for(int i = 1;i <= n;i ++)
        {
            if(d[i] == 1)
                q.add(i);
        }
        while(!q.isEmpty())
        {
            int t = q.poll();
            res --;
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                d[j] --;
                if(d[j] == 1)
                    q.add(j);
            }
        }

        return res;
    }
    public int chaseGame(int[][] edges, int startA, int startB) {
        n = edges.length;
        Arrays.fill(h, -1);
        Arrays.fill(e, 0);
        Arrays.fill(ne, 0);
        Arrays.fill(d, 0);
        idx = 0;
        for(int i = 0;i < n;i ++)
        {
            int a = edges[i][0];
            int b = edges[i][1];
            add(a, b);
            d[b] ++;
            add(b, a);
            d[a] ++;
        }
        bfs(distA, startA);

        bfs(distB, startB);

        int res = topsort();
        int ans = 1;
        if(res == 3)
        {
            for(int i = 1;i <= n;i ++)
            {
                if(distA[i] > distB[i] + 1)
                    ans = Math.max(ans, distA[i]);
            }
        }
        else
        {
            for(int i = 1;i <= n;i ++)
            {
                if(distA[i] > distB[i] + 1)
                {
                    if(d[i] > 1)
                    {
                        ans = -1;
                        break;
                    }
                    else ans = Math.max(ans, distA[i]);
                }
            }
        }
        return ans;
    }
}