SG函数解决结合Nim

sg函数介绍：

SG函数
在有向图游戏中，对于每个节点x，设从x出发共有k条有向边，分别到达节点y1, y2, ...,
yk，定义SG(x)为x的后继节点y1, y2, ..., yk 的SG函数值构成的集合再执行mex(S)运算的结果，即：
        SG(x) = mex({SG(y1), SG(y2), ..., SG(yk)})
特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

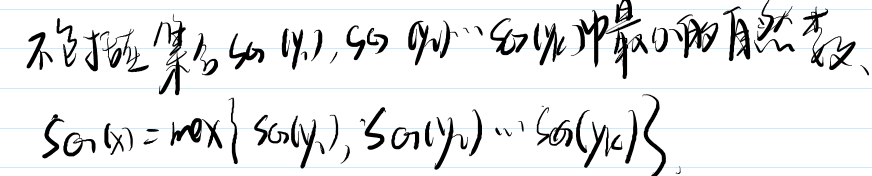
题目分析：

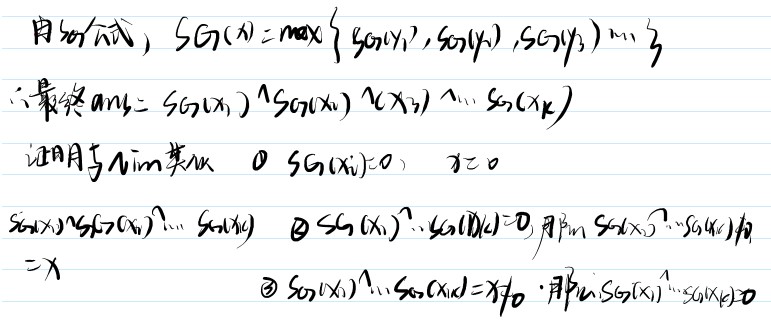
思路：

求sg思路：
f[x]存放sg(x)的结果。
1.记忆化搜索，如果状态已经被计算过了，直接返回。
2.循环每次能拿的石子次数：
使用哈希表存放所有可以到达的状态，使用sum存放集合的点个数，如果当前的数 x大于可以拿的个数，记录状态x - sum（sg(x - sum)）
3.循环i，如果i在哈希表中不存在，那么sg()就是当前的值（sg函数：存放不能到达状态的最小值。）

样例

2
2 5
3
2 4 7

算法1

(Nim + SG函数)

#include<iostream>
#include<unordered_set>
#include<cstring>
using namespace std;
const int N= 100010;
int s[N], f[N], n;
int sg(int x)
{
    unordered_set<int> S;
    if(f[x] != -1)return f[x];
    for(int i = 0; i < n; ++i)
    {
        int c = s[i];
        if(x >= c)S.insert(sg(x - c));
    }
    for(int i = 0; ; ++i)
    {
        if(!S.count(i))
        {
            return f[x] = i;
        }
    }
}

int main()
{
    cin >> n;int m;
    for(int i = 0; i < n; ++i)
    {
        int x; cin >> x;
        s[i] = x;   
    }
    memset(f, -1, sizeof f);
    int res = 0;
    cin >> m;
    for(int i = 0; i < m; ++i)
    {
        int x; cin >> x;
        res ^= sg(x);
    }
    if(res)puts("Yes");
    else puts("No");
    return 0;
}