题目描述

给定一个 points 数组，表示 2D 平面上的一些点，其中 points[i] = [x_i, y_i]。

连接点 [x_i, y_i] 和点 [x_j, y_j] 的费用为它们之间的 曼哈顿距离：|x_i - x_j| + |y_i - yj|，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

样例

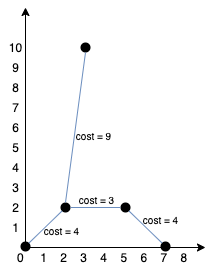
输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：我们可以按照上图所示连接所有点得到最小总费用，总费用为 20。
注意到任意两个点之间只有唯一一条路径互相到达。

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000

输入：points = [[0,0]]
输出：0

限制

• 1 <= points.length <= 1000
• -10^6 <= x_i, y_i <= 10^6
• 所有点 (x_i, y_i) 两两不同。

算法

(最小生成树) $O(n^2)$

1. 完全图下的最小生成树，推荐使用 Prim 算法。

时间复杂度

• $n$ 次迭代，每次需要 $n$ 次循环找最短距离，故总时间复杂度为 $O(n^2)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储 Prim 算法的数据结构。

C++ 代码

class Solution {
private:
    int calc(vector<int> &x, vector<int> &y) {
        return abs(x[0] - y[0]) + abs(x[1] - y[1]);
    }

public:
    int minCostConnectPoints(vector<vector<int>>& points) {
        const int n = points.size();
        vector<bool> vis(n, false);
        vector<int> dis(n, INT_MAX);
        int ans = 0;

        dis[0] = 0;
        for (int i = 0; i < n; i++) {
            int mindis = INT_MAX;
            int m = -1;
            for (int j = 0; j < n; j++)
                if (!vis[j] && mindis > dis[j]) {
                    mindis = dis[j];
                    m = j;
                }

            vis[m] = true;
            ans += mindis;
            for (int j = 0; j < n; j++)
                dis[j] = min(dis[j], calc(points[m], points[j]));
        }

        return ans;
    }
};