题目描述

秋游中的小力和小扣设计了一个追逐游戏。他们选了秋日市集景区中的 N 个景点，景点编号为 1 到 N。此外，他们还选择了 N 条小路，满足任意两个景点之间都可以通过小路互相到达，且不存在两条连接景点相同的小路。整个游戏场景可视作一个无向连通图，记作二维数组 edges，数组中以 [a,b] 形式表示景点 a 与景点 b 之间有一条小路连通。

小力和小扣只能沿景点间的小路移动。小力的目标是在最快时间内追到小扣，小扣的目标是尽可能延后被小力追到的时间。游戏开始前，两人分别站在两个不同的景点 startA 和 startB。每一回合，小力先行动，小扣观察到小力的行动后再行动。小力和小扣在每回合可选择以下行动之一：

• 移动至相邻景点
• 留在原地

如果小力追到小扣（即两人于某一时刻出现在同一位置），则游戏结束。若小力可以追到小扣，请返回最少需要多少回合；若小力无法追到小扣，请返回 -1。

注意：小力和小扣一定会采取最优移动策略。

样例

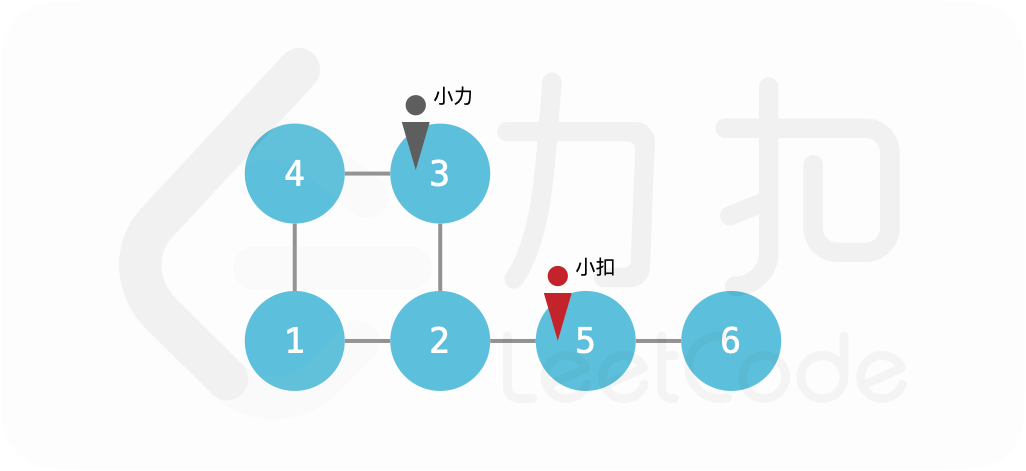
输入：edges = [[1,2],[2,3],[3,4],[4,1],[2,5],[5,6]], startA = 3, startB = 5
输出：3
解释：
第一回合，小力移动至 2 号点，小扣观察到小力的行动后移动至 6 号点；
第二回合，小力移动至 5 号点，小扣无法移动，留在原地；
第三回合，小力移动至 6 号点，小力追到小扣。返回 3。

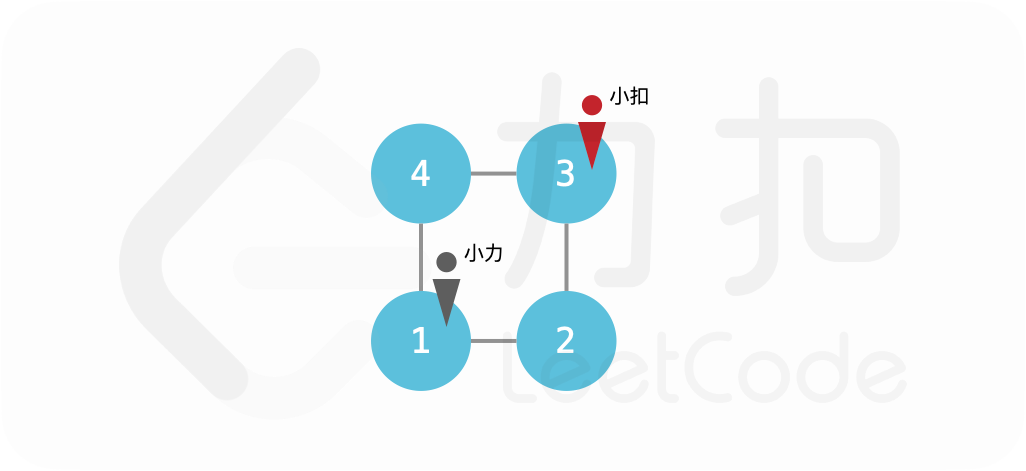
输入：edges = [[1,2],[2,3],[3,4],[4,1]], startA = 1, startB = 3
输出：-1
解释：
小力如果不动，则小扣也不动；否则小扣移动到小力的对角线位置。这样小力无法追到小扣。

限制

• edges 的长度等于图中节点个数。
• 3 <= edges.length <= 10^5
• 1 <= edges[i][0], edges[i][1] <= edges.length 且 edges[i][0] != edges[i][1]
• 1 <= startA, startB <= edges.length 且 startA != startB

算法

(图论，图上寻环) $O(n)$

1. 注意到边的个数等于点的个数，且是一个连通图，所以这个图中有且仅有一个简单环，环的长度大于等于 3。
2. 如果环的长度大于 3，且 B 可以比 A 先到环上，则可以证明 A 无法追到 B。否则，A 一定可以追到 B。
3. 具体实现如下
   • 求出 A 和 B 到每个点的最短距离。
   • 通过 BFS 或者 DFS 找到唯一的环。
   • 如果环大于 3 且存在一个环上的点 x，满足 A 到 x 的最短距离严格大于 B 到 x 的最短距离加 1，则返回 -1。这是因为 B 可以逃到 x 上且过程中 A 无法追到。
   • 其他情况下，初始化答案为 1。然后枚举任意一个点 x，如果满足 A 到 x 的最短距离严格大于 B 到 x 的最短距离加 1，则点 x 可以作为 B 最后的被追到的点，用 A 到 x 的距离更新答案。

时间复杂度

• 预处理和找环的的时间复杂度均为 $O(n)$。
• 枚举点时，判断每个点的复杂度为常数，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储预处理的数据结构。

C++ 代码

class Solution {
private:
    vector<vector<int>> graph;
    stack<int> st;
    vector<bool> inCycle;
    int cycleSize;

    void bfs(int s, vector<int> &dis) {
        dis[s] = 0;
        queue<int> q;
        q.push(s);

        while (!q.empty()) {
            int u = q.front();
            q.pop();
            for (int v : graph[u])
                if (dis[v] > dis[u] + 1) {
                    dis[v] = dis[u] + 1;
                    q.push(v);
                }
        }
    }

    bool dfs(int u, int fa, vector<bool> &inStack) {
        st.push(u);
        inStack[u] = true;

        for (int v : graph[u]) {
            if (v == fa) continue;
            if (inStack[v]) {
                int x;
                do {
                    x = st.top();
                    st.pop();
                    cycleSize++;
                    inCycle[x] = true;
                } while (x != v);

                return true;
            }

            if (dfs(v, u, inStack))
                return true;
        }

        inStack[u] = false;
        st.pop();
        return false;
    }

public:
    int chaseGame(vector<vector<int>>& edges, int startA, int startB) {
        const int n = edges.size();
        graph.resize(n + 1);
        for (const auto &e : edges) {
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
        }

        vector<int> disA(n + 1, INT_MAX), disB(n + 1, INT_MAX);
        bfs(startA, disA);
        bfs(startB, disB);

        vector<bool> inStack(n + 1, false);
        inCycle.resize(n + 1, 0);
        cycleSize = 0;
        dfs(1, 0, inStack);

        if (cycleSize > 3) {
            for (int i = 1; i <= n; i++)
                if (inCycle[i] && disA[i] > disB[i] + 1)
                    return -1;
        }

        int ans = 1;
        for (int i = 1; i <= n; i++)
            if (disA[i] > disB[i] + 1)
                ans = max(ans, disA[i]);

        return ans;
    }
};