$x$ 个 $8$ 连在一起组成的正整数可以写成
$$ 8 \times \frac{10^x - 1}{9} $$

求最小的 $x$，满足 $9L \mid 8(10^x - 1)$
$\textbf{let } d = \textbf{gcd}(L, 8)$
$$ \Longrightarrow \frac{9L}{d} \mid (10^x -1) \Rightarrow 10^x \equiv 1 (\bmod \frac{9L}{d}) $$

引理，若 $(a, n)=1$，则满足 $a^x \equiv 1 (\bmod n)$ 的最小正整数 $x_0$，满足
$x_0 \mid \phi(n)$
proof
反证法，不妨设 $\phi(n) = qx_0 + r \quad (0 < r < x_0)$
$a^{x_0} \equiv 1 (\bmod n) \Rightarrow a^{qx_0} \equiv 1(\bmod n)$
根据欧拉定理，有 $a^{\phi(n)} \equiv 1(\bmod n)$
$$ \begin{cases} a^{qx_0} \equiv 1 (\bmod n) \\\ a^{\phi(n)} \equiv 1 (\bmod n) \end{cases} \Rightarrow a^{r} \equiv 1(\bmod n) \Rightarrow r < x_0 $$
矛盾

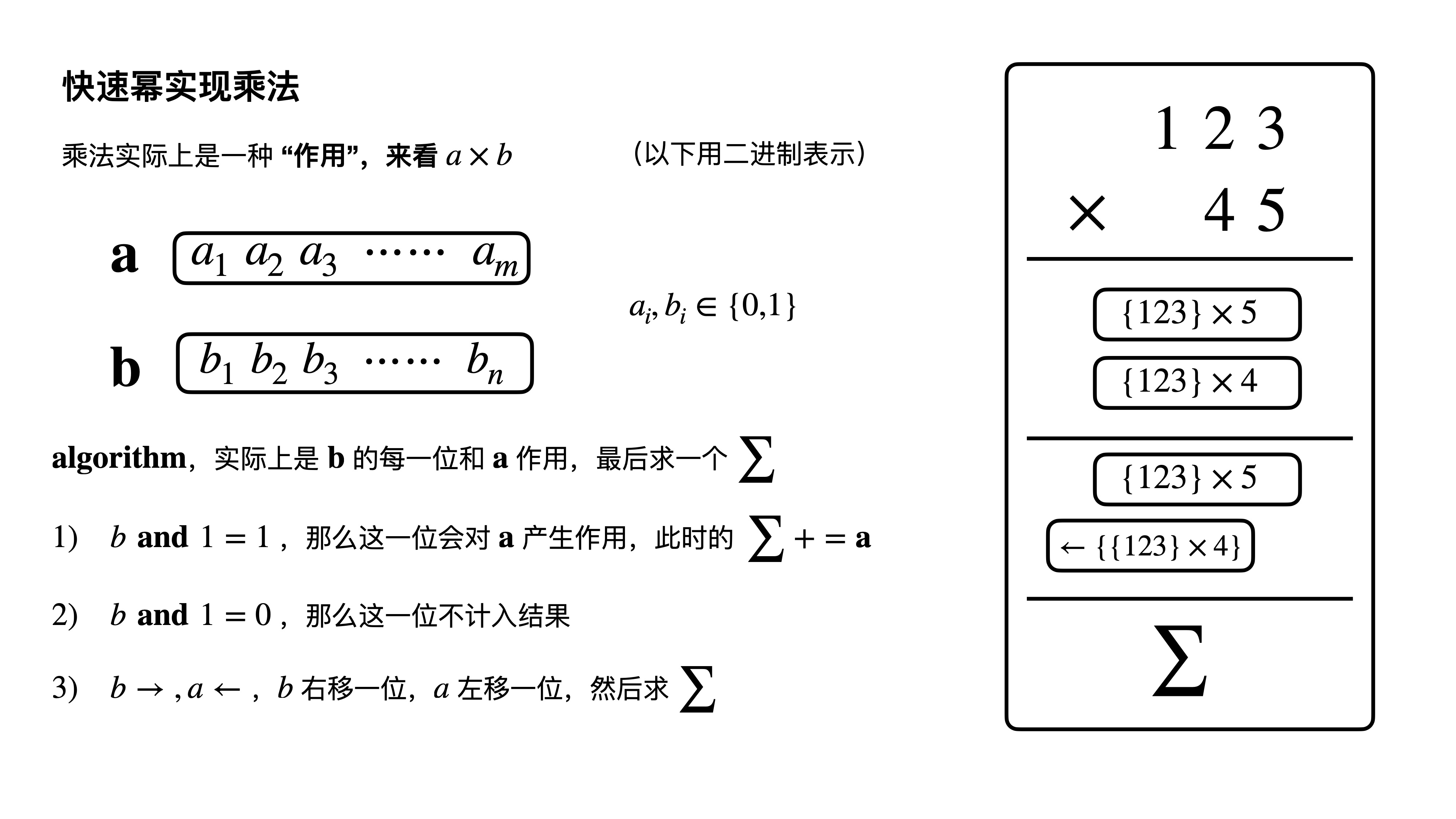
先重温一下快速幂

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
#include <cmath>
#include <bitset>
#include <assert.h>

using namespace std;
typedef long long ll;
typedef set<int>::iterator ssii;

#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(b))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
#define MPR(a, b) make_pair(a, b)

pair<int, int> crack(int n) {
    int st = sqrt(n);
    int fac = n / st;
    while (n % st) {
        st += 1;
        fac = n / st;
    }

    return make_pair(st, fac);
}


template <class T>
inline bool chmax(T& a, T b) {
    if(a < b) {
        a = b;
        return true;
    }
    return false;
}

template <class T>
inline bool chmin(T& a, T b) {
    if(a > b) {
        a = b;
        return true;
    }
    return false;
}

bool _check(int x) {
    //
    return true;
}

int bsearch1(int l, int r) {
    while (l < r) {
        int mid = (l + r) >> 1;
        if(_check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

int bsearch2(int l, int r) {
    while (l < r) {
        int mid = (l + r + 1) >> 1;
        if(_check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

// ============================================================== //
ll L;
const ll inf = 1e18;

ll gcd(ll a, ll b) {
    return b == 0 ? a : gcd(b, a % b);
}

ll ksc(ll a, ll b, ll mod) {
    ll ans = 0;
    for(; b; b >>= 1) {
        if (b & 1) ans = (ans + a) % mod;
        a = (a * 2) % mod;
    }
    return ans;
}

ll ksm(ll a, ll b, ll mod) {
    ll ans = 1 % mod;
    a %= mod;

    for(; b; b >>= 1) {
        if (b & 1) ans = ksc(ans, a, mod);
        a = ksc(a, a, mod);
    }

    return ans;
}


ll phi(ll n) {
    ll ans = n;
    for(ll i = 2; i * i <= n; i++) {
        if (n % i == 0) {
            ans = ans / i * (i - 1);
            while (n % i == 0) n /= i;
        }
    }

    if (n > 1) ans = ans / n * (n - 1);
    return ans;
}

ll solve() {
    ll d = gcd(L, 8ll);
    ll mod = 9 * L / d;

    if (gcd(mod, 10ll) != 1) return 0;

    ll N = phi(mod);
    ll res = inf;

    for(ll i = 1; i <= sqrt(N); i++) {
        if (N % i) continue;
        if (ksm(10ll, i, mod) == 1) chmin(res, i);
        if (ksm(10ll, N/i, mod) == 1) chmin(res, N/i);
    }

    return res == inf ? 0 : res;
}

int main() {
    //freopen("input.txt", "r", stdin);
    int kase = 0;
    while (cin >> L && L) {
        printf("Case %d: ", ++kase);

        ll res = solve();
        printf("%lld\n", res);
    }
}