题目描述

给你一个奇怪的打印机，它有如下两个特殊的打印规则：

• 每一次操作时，打印机会用同一种颜色打印一个矩形的形状，每次打印会覆盖矩形对应格子里原本的颜色。
• 一旦矩形根据上面的规则使用了一种颜色，那么 相同的颜色不能再被使用。

给你一个初始没有颜色的 m x n 的矩形 targetGrid，其中 targetGrid[row][col] 是位置 (row, col) 的颜色。

如果你能按照上述规则打印出矩形 targetGrid，请你返回 true，否则返回 false。

样例

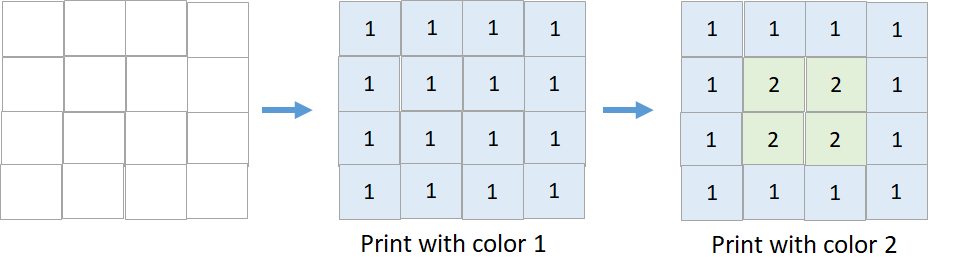
输入：targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
输出：true

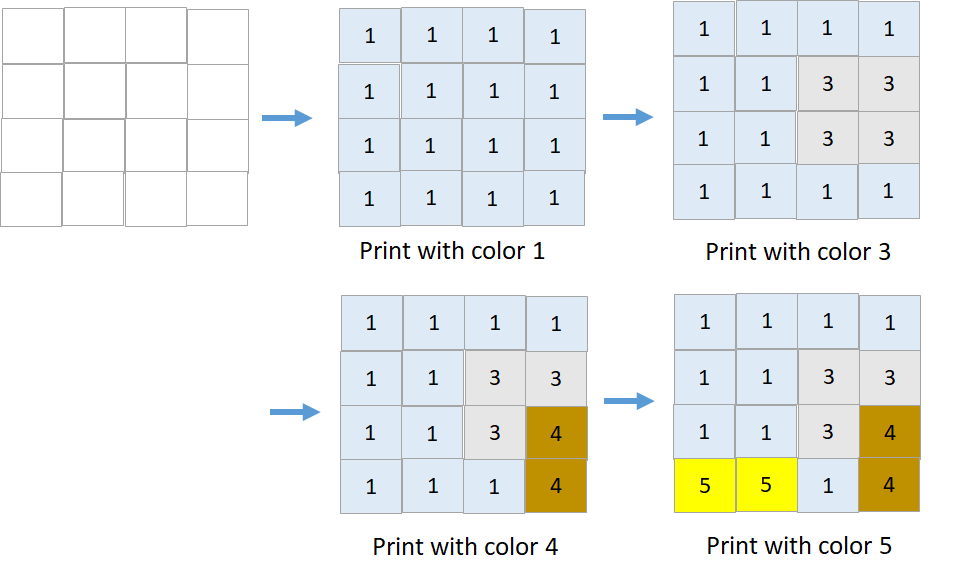
输入：targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
输出：true

输入：targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
输出：false
解释：没有办法得到 targetGrid ，因为每一轮操作使用的颜色互不相同。

输入：targetGrid = [[1,1,1],[3,1,3]]
输出：false

限制

• m == targetGrid.length
• n == targetGrid[i].length
• 1 <= m, n <= 60
• 1 <= targetGrid[row][col] <= 60

算法

(拓扑排序) $O(c(mn + c))$

1. 对于每种颜色 $u$，求出其左上的位置和右下的位置。然后遍历以这两个位置确定的子矩形，对于其中的其他颜色 $v$，建立一条 $u$ 到 $v$ 的边。
2. 拓扑排序，判断是否存在环。

时间复杂度

• 假设共有 $c$ 种颜色，每种颜色需要 $O(mn)$ 的时间构建边，这需要 $O(cmn)$ 的时间复杂度，共有 $O(c^2)$ 条边。
• 拓扑排序的时间复杂度等于边数，故总时间复杂度为 $O(c(mn + c))$。

空间复杂度

• 需要 $O(c^2)$ 的额外空间存储整张图和存储拓扑排序的数据结构。

C++ 代码

class Solution {
private:
    int m, n, c;

    void build(int u, const vector<vector<int>> &targetGrid,
               vector<vector<int>> &graph, vector<int> &indeg) {
        int x1 = INT_MAX, y1 = INT_MAX, x2 = INT_MIN, y2 = INT_MIN;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (targetGrid[i][j] == u) {
                    x1 = min(x1, i); y1 = min(y1, j);
                    x2 = max(x2, i); y2 = max(y2, j);
                }

        if (x1 == INT_MAX)
            return;

        vector<bool> vis(c + 1, false);
        vis[u] = true;
        for (int i = x1; i <= x2; i++)
            for (int j = y1; j <= y2; j++) {
                int v = targetGrid[i][j];
                if (vis[v]) continue;
                vis[v] = true;
                graph[u].push_back(v);
                indeg[v]++;
            }
    }

public:
    bool isPrintable(vector<vector<int>>& targetGrid) {
        m = targetGrid.size();
        n = targetGrid[0].size();
        c = 60;

        vector<vector<int>> graph(c + 1);
        vector<int> indeg(c + 1, 0);

        for (int i = 1; i <= c; i++) {
            build(i, targetGrid, graph, indeg);
        }

        queue<int> q;
        for (int i = 1; i <= c; i++) {
            if (indeg[i] == 0)
                q.push(i);
        }

        int tot = 0;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            tot++;

            for (int v : graph[u]) {
                indeg[v]--;
                if (indeg[v] == 0)
                    q.push(v);
            }
        }

        return tot == c;
    }
};