思路：

求最小生成树，就是求和已经在生成树中的点的距离最小的点不断加到生成树中，直到所有点都加进去。
考虑并查集的思想
按照从小到大的顺序排序边权值。
1.并利用并查集的性质，如果当前的点和并查集里面的点有边关联，那么加上边权值，相当于生成树中的两个点和边。
2.再把当前的点加入到集合中，后面的点再加进来肯定和集合中（生成树的点有关联）。

模拟：

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

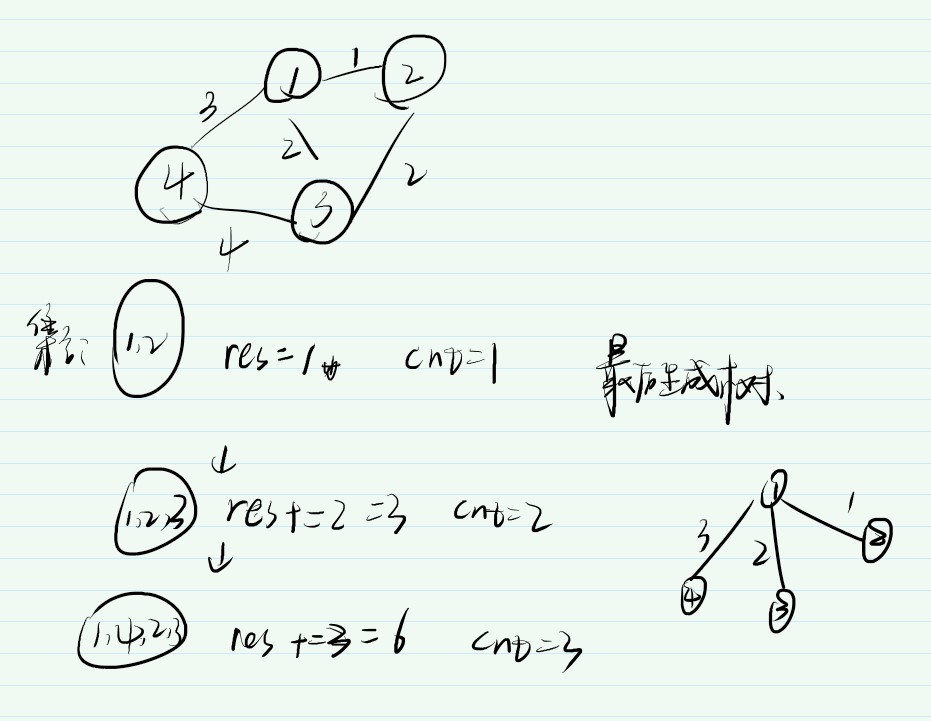
代码o(mlogm)

/
易错点：
1.if(cnt >= n - 1)return res; cnt计算的是边的数量
2.for(int i = 0; i < m; ++i) 在赋给结构体值得时候，第一条边得下标是0，因此后面并查集操作得时候也要从0开始
/

include[HTML_REMOVED]

include[HTML_REMOVED]

using namespace std;
const int N = 200010;
int n, m, p[N];
struct edge{
int a, b, w;
bool operator <(const edge & e)const
{
return w < e.w;
}
}edges[N];

int find(int u)
{
if(u != p[u])p[u] = find(p[u]);
return p[u];
}
int kruskal()
{
int res = 0 , cnt = 0;
/按权重从小到大排序/
sort(edges, edges + m);
/初始画并查集/
for(int i = 1; i <= n; i)
{
p[i] = i;
}
for(int i = 0; i < m; i)
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a);b = find(b);
if(a != b)
{
res += w;
/只有当所有的边都加进来才能算是无向图的生成树/
cnt ++;
p[a] = b;
// cout << res << endl;
}
}
/n个点，n-1 条边/
if(cnt >= n - 1)return res;
else return -1;
}

int main()
{
int a, b,c;
cin >> n >> m;
for(int i = 0; i < m; ++i)
{
cin >> a >> b >> c;
edges[i] = {a, b, c};
}
int ans = kruskal();
if(ans == -1)puts(“impossible”);
else printf(“%d”, ans);
return 0;
}