题目描述

给你两组点，其中第一组中有 size1 个点，第二组中有 size2 个点，且 size1 >= size2 。

任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出，其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接，则称这两组点是连通的。换言之，第一组中的每个点必须至少与第二组中的一个点连接，且第二组中的每个点必须至少与第一组中的一个点连接。

返回连通两组点所需的最小成本。

提示：

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

样例

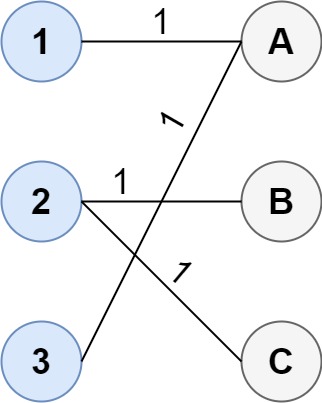
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A ，但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

算法

(状态压缩动态规划) $O(m* n * 2^n)$

设共m行n列，由于数据很小，可以考虑枚举所有第二组点的状态，每个比特位表示第二组的每一列，共1<<n个状态，然后从第一组的每一行开始，逐一计算所需的最小成本。

状态设定与初始化如下：

• 考虑 $costSum[i][s]$ 表示第一组的第i行和第二组的s状态相连时，所需的费用。

• 考虑 $dp[i+1][s]$ 表示从第0行开始，选取至第一组的第i行，此时第一组第0行至第i行所有点，与第二组相连的状态为s时，所需的费用。

算法过程如下：

1. 初始化 costSum 数组。
2. 对第一组的第i行，枚举至此与第二组相连的所有可能的状态s1。把第i行与第二组的至少一个点相连，保证第i行至少有一条边能连上；考虑状态s1以外无连线的状态s2，若将状态s2与第i行相连的最小值。
3. 最后返回dp[m][(1<<n)-1]即为考虑了所有m行且与第二组所有点相连的结果。

感觉有点绕，不好说清楚，我也是看了比赛里结果里的大佬的代码改出来的Orz

时间复杂度

初始化costSum数组需要$O(m*2^n)$；

dp状态转移需要$O(m * n * 2^n)$。

C++ 代码

class Solution {
public:
    int connectTwoGroups(vector<vector<int>>& cost) {
        int m=cost.size(), n=cost[0].size();
        const int inf=1<<30;

        vector<vector<int>> costSum(m, vector<int>(1<<n));
        for(int i=0;i<m;i++){
            for(int s=0;s<(1<<n);s++){
                for(int j=0;j<n;j++){
                    if((s>>j)&1) costSum[i][s]+=cost[i][j];
                }
            }
        }
        vector<vector<int>> dp(m+1, vector<int>(1<<n, inf));
        dp[0][0]=0;
        for(int i=0;i<m;i++){
            for(int s1=0;s1<(1<<n);s1++){
                // 至少与第二组的1点相连
                for(int j=0;j<n;j++){
                    dp[i+1][s1|(1<<j)] = min(dp[i+1][s1|(1<<j)], dp[i][s1]+cost[i][j]);
                }
                // 考虑第二组中没有相连的点
                int state = ((1<<n)-1)^s1;
                for(int s2=state ; s2 ; s2=(s2-1)&state){
                    dp[i+1][s1|s2]=min(dp[i+1][s1|s2], dp[i][s1]+costSum[i][s2]);
                }
            }
        }


        return dp[m][(1<<n)-1];
    }
};