分析：

用小根堆存储每一组的最大右端点。
只要有交集就判断：
如果堆中最小右端点  > =L[i](当前组的左端点)，说明有交集，开一个新组。
如果都没有交集，加入结果中，说明可以加入到已有组内部（满足两两互不相交）（更新当前组的右端点）。
最后组的数量就是答案。（证明如下：）

思路：

思路：
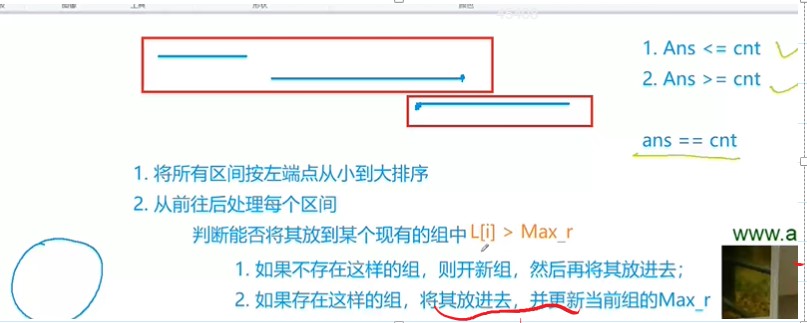
1.所有区间按左端点从小到大排序
2.用小根堆存储每一组的最大右端点
遍历每一个区间：
3.如果堆中最小右端点  > =L[i](当前组的左端点)，说明有交集，开一个新组。
4.如果都没有交集，加入结果中，说明可以加入到已有组内部（满足两两互不相交）（更新当前组的右端点）

问题：

1.$\cal{Question:}$
如果有这个区间和当前组中的区间没有交集，但是区间整个区间都在组中最大右端点的区间前面，按照思路新开一个组，这样的组一定是最少的吗？
上述的这种情况不存在。
$\cal{Ans:}$由于按照区间左端点排序，因此后面区间左端点一定 >= 组中的左端点，
如果左端点 > 组中最大的右端点，那么右段点比组中的所有右端点大；
如果相反，那么一定会和组中的区间有交点。

代码

#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
const int N = 100010;
struct range
{
    int l ,r;
    /*所有区间按左端点从小到大排序*/
    bool operator <(const range & w)const
    {
        return l < w.l;
    }
}R[N];
int main()
{
    int n; scanf("%d", &n);
    for(int i = 0; i< n; ++i)
    {
        int a, b; scanf("%d%d", &a, &b);
        R[i] = {a, b};
    }
    sort(R, R + n);
    /*用小根堆存储每一组的最大右端点*/
    priority_queue<int, vector<int>, greater<int>> h;
    for(int i = 0; i < n; ++i)
    {
        /*如果堆中最小右端点  > =L[i](当前组的左端点)，说明有交集，开一个新组。*/
        if(h.empty() || h.top() >= R[i].l)h.push(R[i].r);
        else
        {
            /*如果都没有交集，加入结果中，说明可以加入到已有组内部（满足两两互不相交）（更新当前组的右端点）。*/
            int t = h.top();h.pop();
            h.push(R[i].r);
        }
      //  if(h.size()) cout << h.size() <<endl;
    }
    cout << h.size() <<endl;
    return 0;
}