分析:

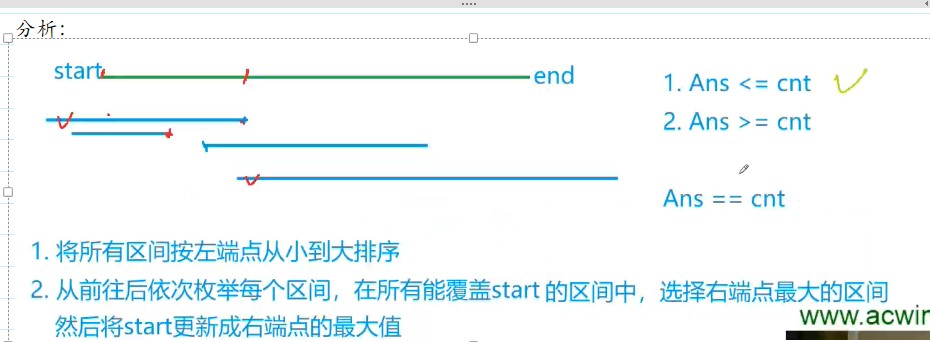
思路：

思路：
1.排序
2.从前往后一次枚举每个区间：判断左端点在st之前的区间，循环找到最大右端点，如果右端点也在st之前，说明无法覆盖。下一次枚举的时候依旧用这个区间(i不变)。
3.如果找到左端点在st之前，右端点在st之后的区间，(i++)
4.每循环一次，没有在前面跳出的话，说明找到了一个区间，res++
5.如果这个区间右端点能覆盖end，说明能覆
6.把start更新成right，保证后面的区间适合之前的区间有交集，从而形成对整个序列的覆盖
7。如果遍历了所有的数组，还是没有覆盖最后的end，说明不能成功

问题

$\cal{Question1:}$为什么要用双指针？
$\cal{Answer:}$不用双指针也可以，直接用i就行

$\cal{Question2:}$为什么right不在循环外面？
$\cal{Answer:}$right必须要在循环内部定义， 每次更新完右端点后，right要设为最小值，否则会把上一次的区间也算进去，这样就不会存在right < st的情况，因为在上一次情况中right = st。

代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100010; 
struct range
{
    int l, r;
    bool operator < (const range &w)const 
    {
        return l < w.l;
    }
}R[N];


int main()
{
    int st, ed;
    cin >> st >> ed;
    int n; cin >> n;
    for(int i = 0; i < n; ++i)
    {
        int x, y; cin >> x >> y;
        R[i] = {x, y};
    }
    sort(R, R +n);
    /*从前往后一次枚举每个区间*/
    int res = 0; bool success = false;
    for(int i = 0; i < n; ++i)
    {
         int j = i, right = 0xc0c0c0c0;
        /*判断左端点在st之前的区间，循环找到最大右端点，如果右端点也在st之前，说明无法覆盖*/
        while(j < n && R[j].l <= st)
        {
            right = max(right, R[j].r);
            j++;
        }
        /*如果右端点也在st之前，说明无法覆盖*/
        if(right < st)
        {
            res = -1;
            break;
        }
        /*每循环一次，没有在前面跳出的话，说明找到了一个区间，res++*/
        res++;
       // cout << j << " " << right << endl;
        /*如果这个区间右端点能覆盖end，说明能覆盖*/
        if(right >= ed)
        {
            success = true;
            break;
        }
        /*把start更新成right，保证后面的区间适合之前的区间有交集，从而形成对整个序列的覆盖*/
        st = right;
        i = j - 1;
    }
    /*如果遍历了所有的数组，还是没有覆盖最后的end，说明不能成功*/
    if(!success)res = -1;
    cout << res <<endl;
    return 0;
}