题目描述

给你一个奇怪的打印机，它有如下两个特殊的打印规则：

• 每一次操作时，打印机会用同一种颜色打印一个矩形的形状，每次打印会覆盖矩形对应格子里原本的颜色。
• 一旦矩形根据上面的规则使用了一种颜色，那么 相同的颜色不能再被使用 。
  给你一个初始没有颜色的 m x n 的矩形 targetGrid ，其中 targetGrid[row][col] 是位置 (row, col) 的颜色。

如果你能按照上述规则打印出矩形 targetGrid ，请你返回 true ，否则返回 false 。

样例

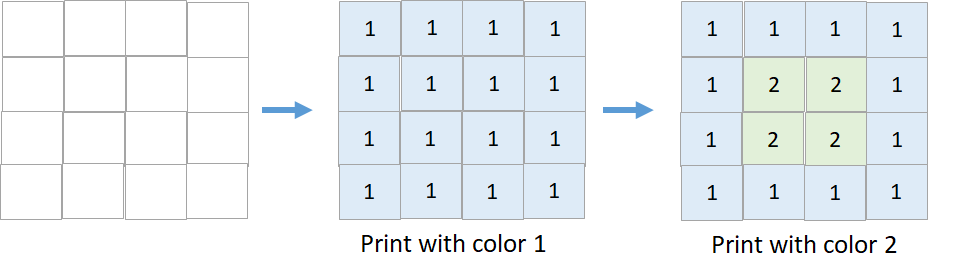
输入：targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
输出：true

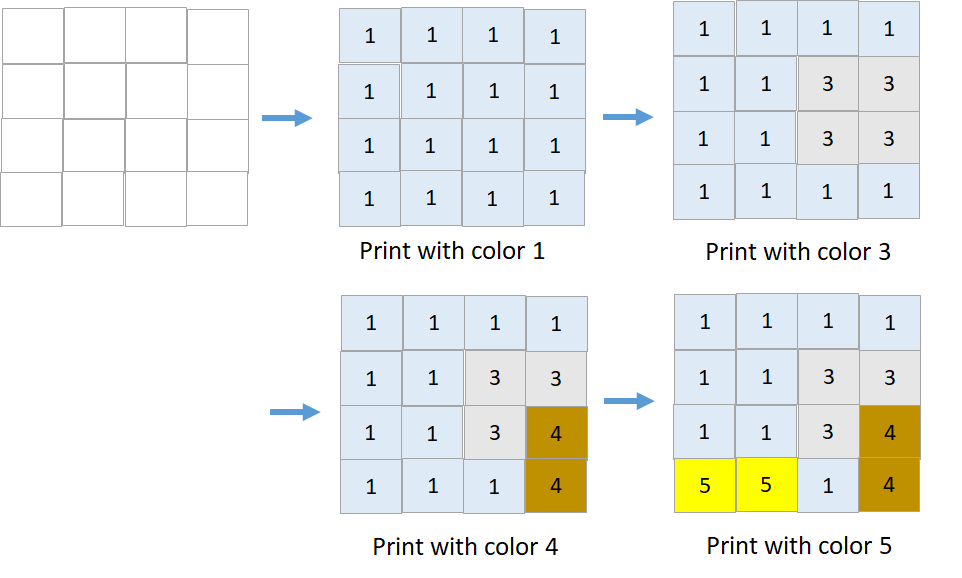
输入：targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
输出：true

输入：targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
输出：false
解释：没有办法得到 targetGrid ，因为每一轮操作使用的颜色互不相同。

输入：targetGrid = [[1,1,1],[3,1,3]]
输出：false

提示：

• m == targetGrid.length
• n == targetGrid[i].length
• 1 <= m, n <= 60
• 1 <= targetGrid[row][col] <= 60

算法分析

拓扑排序

原理：
对于方格上的某一个点，若经过几次染色，例如先染了a颜色，再染了b颜色，最后染了c颜色，那么该点最终表现出来的颜色是c颜色，染的颜色一定是有顺序的这里是顺序是a -> b -> c

在给定的矩阵中，如何找到某两种颜色的先后顺序，计算出每种颜色染颜色的矩形区间，若a颜色和b颜色有重合的格子，且该格子是表现是b颜色，那么一定是a -> b，找到所有的单向关系，题中表示，颜色最多有60种，建立一个有向图，图中的结点数目是60个，编号是1~60。做一遍拓扑排序

操作：

• 1、枚举整个矩阵，找到每种颜色染颜色的最大矩形区间，分别用up[],down[],left[],right[]维护矩形的四个端点
• 2、建图，枚举整个矩形，假设当前格子是颜色是color，枚举所有颜色染的颜色的矩形，若color在k颜色区间内却不为k，则k -> color
• 3、跑一遍拓扑排序，先把入度为0的颜色进入队列，最后观察出队的颜色数量是不是60个，若是表示能打印该矩形，return true，否则return false

注意：每个格子最多连接60条边，最多有60 * 60个格子

时间复杂度 $O(n^3)$

建图时间复杂度$O(n^3)$，拓扑排序时间复杂度$O(n + n^3)$

Java 代码

class Solution {
    static int N = 65, M = N * N * N, INF = 0x3f3f3f3f;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int idx = 0;
    static int[] d = new int[N];//入度
    static void add(int a,int b)
    {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx ++;
    }
    static boolean topsort()
    {
        Queue<Integer> q = new LinkedList<Integer>();
        for(int i = 1;i <= 60;i ++)
            if(d[i] == 0)
                q.add(i);

        int res = 0;
        while(!q.isEmpty())
        {
            int t = q.poll();
            res ++;
            for(int i = h[t];i != -1;i = ne[i])
            {
                int j = e[i];
                d[j] --;
                if(d[j] == 0)
                {
                    q.add(j);
                }
            }
        }
        return res == 60;
    }
    public boolean isPrintable(int[][] targetGrid) {
        int n = targetGrid.length;
        int m = targetGrid[0].length;
        int[] up = new int[N];
        int[] down = new int[N];
        int[] left = new int[N];
        int[] right = new int[N];
        Arrays.fill(up, INF);
        Arrays.fill(down,-INF);
        Arrays.fill(left, INF);
        Arrays.fill(right, -INF);
        Arrays.fill(h, -1);
        Arrays.fill(e, 0);
        Arrays.fill(ne, 0);
        Arrays.fill(d, 0);

        for(int i = 0;i < n;i ++)
            for(int j = 0;j < m;j ++)
            {
                int x = targetGrid[i][j];
                up[x] = Math.min(up[x], i);
                down[x] = Math.max(down[x], i);
                left[x] = Math.min(left[x], j);
                right[x] = Math.max(right[x], j);
            }

        idx = 0;
        for(int i = 0;i < n;i ++)
            for(int j = 0;j < m;j ++)
            {
                int color = targetGrid[i][j];
                for(int k = 1;k <= 60;k ++)
                {
                    if(k == color) continue;
                    //若color在k颜色区间内却不为k，则k -> color
                    if(i >= up[k] && i <= down[k] && j >= left[k] && j <= right[k])
                    {
                        add(k, color);
                        d[color] ++;
                    }
                }
            }

        return topsort();
    }
}