题目描述

给你两组点，其中第一组中有 size1 个点，第二组中有 size2 个点，且 size1 >= size2 。

任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出，其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接，则称这两组点是连通的。换言之，第一组中的每个点必须至少与第二组中的一个点连接，且第二组中的每个点必须至少与第一组中的一个点连接。

返回连通两组点所需的最小成本。

样例

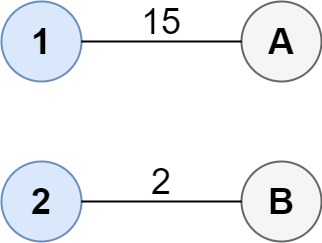
输入：cost = [[15, 96], [36, 2]]
输出：17
解释：连通两组点的最佳方法是：
1--A
2--B
总成本为 17 。

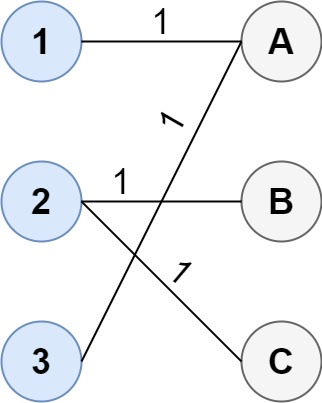
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A ，
但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

输入：cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出：10

提示：

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

算法分析

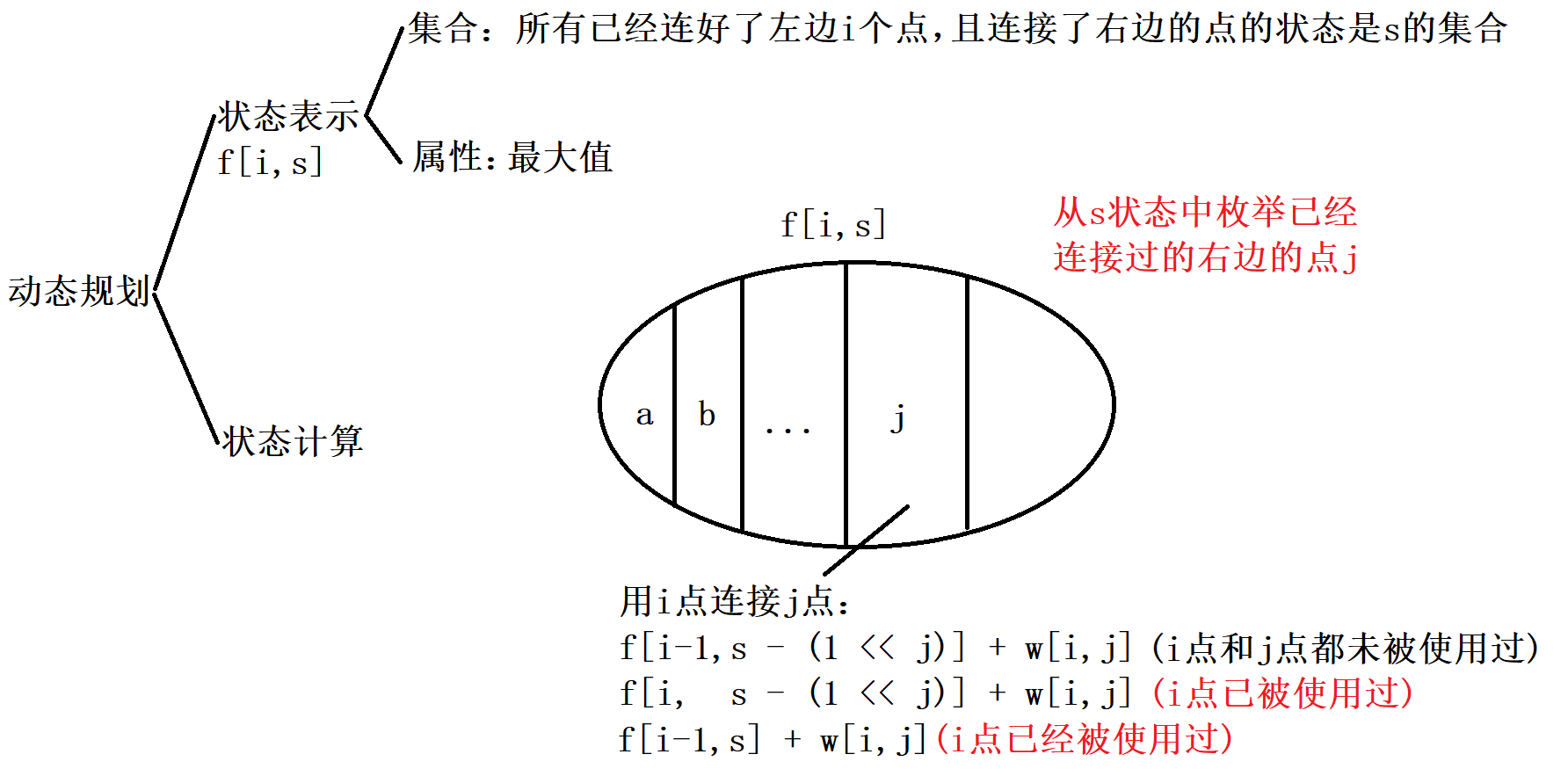
笔误：图中3条方程中最后一条是f[i - 1][s] + w[i][j] （j 点已经被使用过，是 j 点不是 i 点）

时间复杂度 $O(nm2^m)$

空间复杂度 $O(n2^m)$

由于第i层只依赖第i层和第i - 1层，因此可以优化到一维，空间复杂度优化到$O(2^m)$

Java 代码

class Solution {
    static int N = 13, M = 1 << N;
    static int INF = 0x3f3f3f3f;
    public int connectTwoGroups(List<List<Integer>> cost) {
        int n = cost.size();
        int m = cost.get(0).size();
        int[][] f = new int[N][M];
        for(int i = 0;i <= n;i ++) Arrays.fill(f[i], INF);
        f[0][0] = 0;
        for(int i = 1;i <= n;i ++)
            for(int s = 0;s < 1 << m;s ++)
                for(int j = 0;j < m;j ++)
                {
                    if(((s >> j) & 1) == 1)
                    {
                        f[i][s] = Math.min(f[i][s], f[i - 1][s - (1 << j)] + cost.get(i - 1).get(j));
                        f[i][s] = Math.min(f[i][s], f[i][s - (1 << j)] + cost.get(i - 1).get(j));
                        f[i][s] = Math.min(f[i][s], f[i - 1][s] + cost.get(i - 1).get(j));
                    }
                }
        return f[n][(1 << m) - 1];
    }
}

Java 代码（另外一种写法）

class Solution {
    static int N = 13, M = 1 << N;
    static int INF = 0x3f3f3f3f;
    public int connectTwoGroups(List<List<Integer>> cost) {
        int n = cost.size();
        int m = cost.get(0).size();
        int[][] f = new int[N][M];
        for(int i = 0;i <= n;i ++) Arrays.fill(f[i], INF);
        f[0][0] = 0;
        //第i个点连接j点（i点未被使用过）
        //第i个点连接j点（i点已经被使用过）
        for(int i = 0;i < n;i ++)
            for(int s = 0;s < 1 << m;s ++)
                for(int j = 0;j < m;j ++)//若连接右边j这个点
                {
                    f[i + 1][s | (1 << j)] = Math.min(f[i + 1][s | (1 << j)], f[i][s] + cost.get(i).get(j));
                    f[i + 1][s | (1 << j)] = Math.min(f[i + 1][s | (1 << j)], f[i + 1][s] + cost.get(i).get(j));
                    f[i + 1][s | (1 << j)] = Math.min(f[i + 1][s | (1 << j)], f[i][s | (1 << j)] + cost.get(i).get(j));
                }
        return f[n][(1 << m) - 1];
    }
}