裴蜀定理：

对于任意正整数a，b，一定存在非零数对（x,y),满足ax+by=gcd(a,b)

对于任意的数对满足ax+by=d，则d一定是gcd的倍数，自己动手化简

扩展欧几里得算法实在利用递归的求法求解系数x，y；

设int exgcd(a,b,x,y)是求解系数x,y的函数，返回值是gcd（a,b)，那么可以根据递归求出exacd（b,a%b,i,j)求出系数i，j

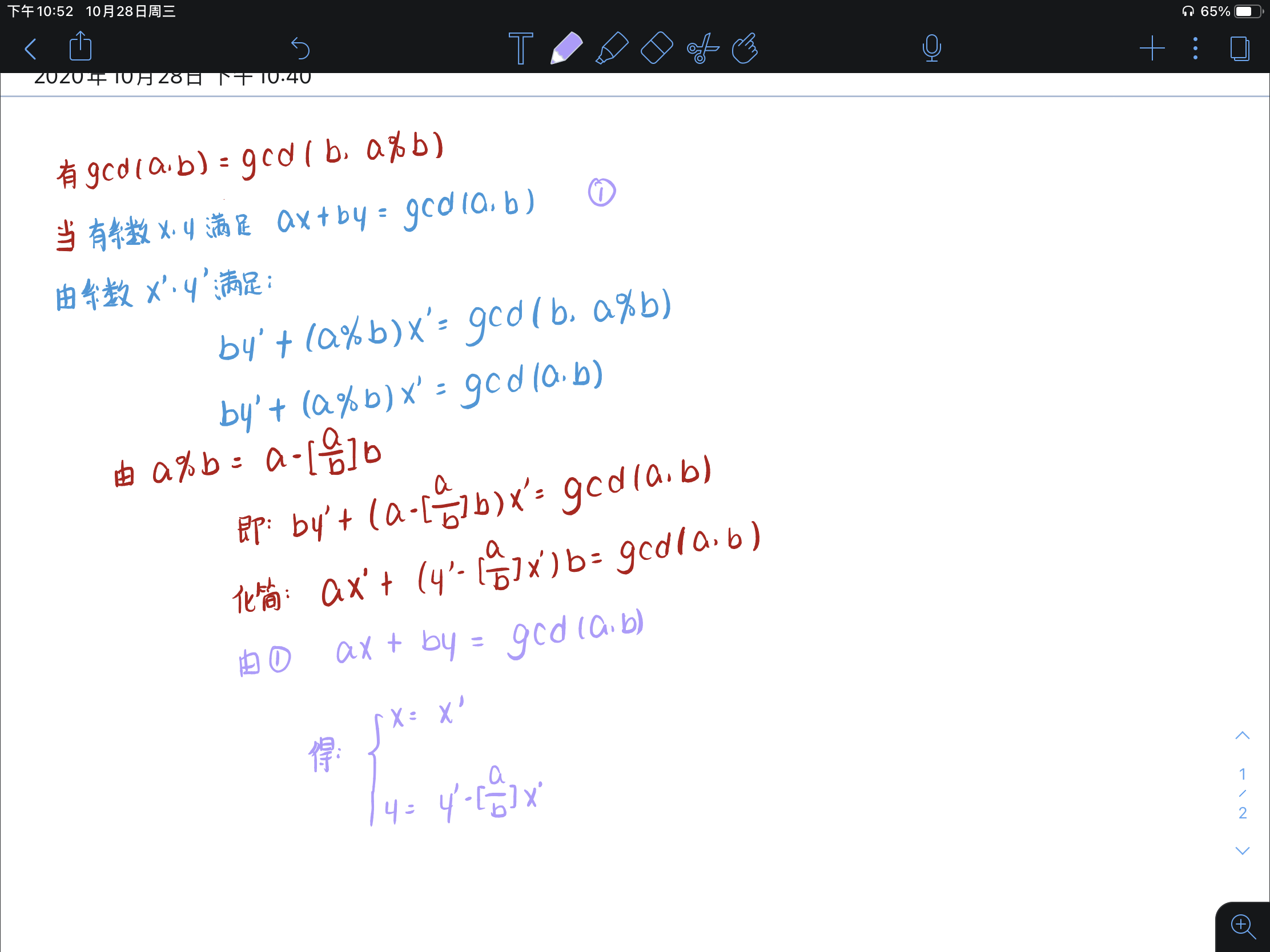
根据下面的推导得到x，y与i，j的关系：

C++代码：

#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y)//传的是引用
{
    if(!b){
      x=1,y=0;
      return a;
    }
    int d=exgcd(b,a%b,y,x);//这里会有系数变换
    y-=a/b*x;
    return d;
}
int main()
{
    int n;
    cin>>n;
    while(n--){
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
    return 0;
}