题目描述

给定两组点，其中第一组中有 size1 个点，第二组中有 size2 个点，且 size1 >= size2。

任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出，其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接，则称这两组点是连通的。换言之，第一组中的每个点必须至少与第二组中的一个点连接，且第二组中的每个点必须至少与第一组中的一个点连接。

返回连通两组点所需的最小成本。

样例

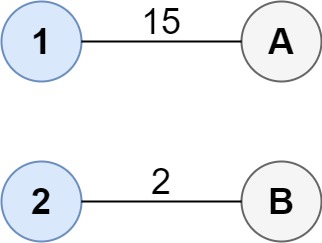
输入：cost = [[15, 96], [36, 2]]
输出：17
解释：连通两组点的最佳方法是：
1--A
2--B
总成本为 17。

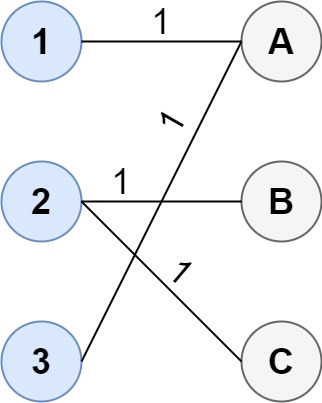
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A，
但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

输入：cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出：10

限制

• size1 == cost.length
• size2 == cost[i].length
• 1 <= size1, size2 <= 12
• size1 >= size2
• 0 <= cost[i][j] <= 100

算法1

(状态压缩动态规划) $O(nm \cdot 2^m + n \cdot 3^m)$

1. 设状态 $f(i, s)$ 表示连接了第一组的前 $i$ 个点，此时第二组的连通的状态为 $s$。$i$ 的有效下标从 1 开始。$s$ 是一个二进制数字，其 01 分别表示连通和未联通。
2. 初始时 $f(0, 0) = 0$，其余为无穷。
3. 转移时，对于状态 $f(i, s)$
   • 假设 $sub$ 是 $s$ 的一个子集，则可以转移 $f(i, s) = \min(f(i, s), f(i - 1, s \text{xor} sub) + c(i, sub))$，即第一组的点 $i$ 连接第二组 $sub$ 的点。其中 $c(i, sub)$ 表示第一组的点 $i$ 连接第二组 $sub$ 的点的总代价。
   • 第一组的点 $i$ 也可以只连接第二组的任意一个点，转移 $f(i, s | (1 << j)) = \min(f(i, s | (1 << j)), f(i - 1, s) + cost(i, j))$。
4. 最终答案为 $f(n, (1 << m) - 1)$。

时间复杂度

• 状态数共 $O(n \cdot 2^m)$，预处理需要 $O(nm \cdot 2^m)$，转移需要 $O(m \cdot 2^m + 3^m)$，故总时间复杂度为 $O(nm \cdot 2^n + n \cdot 3^m)$。

空间复杂度

• 需要 $O(n \cdot 2^m)$ 的额外空间存储状态和预处理的代价数组。

C++ 代码

class Solution {
public:
    int connectTwoGroups(vector<vector<int>>& cost) {
        const int n = cost.size(), m = cost[0].size();
        const int INF = 1000000000;
        vector<vector<int>> f(n + 1, vector<int>(1 << m, INF));
        vector<vector<int>> c(n + 1, vector<int>(1 << m, 0));

        for (int i = 1; i <= n; i++) {
            c[i][0] = INF;
            for (int s = 1; s < (1 << m); s++)
                for (int j = 0; j < m; j++)
                    if ((s >> j) & 1)
                        c[i][s] += cost[i - 1][j];
        }

        f[0][0] = 0;
        for (int i = 1; i <= n; i++)
            for (int s = 1; s < (1 << m); s++) {
                for (int sub = s; sub; sub = (sub - 1) & s)
                    f[i][s] = min(f[i][s], f[i - 1][s ^ sub] + c[i][sub]);

                for (int j = 0; j < m; j++)
                    f[i][s | (1 << j)] = min(f[i][s | (1 << j)],
                                             f[i - 1][s] + cost[i - 1][j]);
            }


        return f[n][(1 << m) - 1];
    }
};

算法2

(状态压缩动态规划) $O(nm \cdot 2^m)$

1. 状态表示和初始化算法 1 一样。
2. 对于第一组的点 $i$ 来说，连接到第二组的点集的代价与点连接的顺序无关，所以可以优化转移，不再需要枚举子集。
3. 转移时
   • 第一组的点 $i$ 只连接第二组的任意一个点，转移 $f(i, s | (1 << j)) = \min(f(i, s | (1 << j)), f(i - 1, s) + cost(i, j))$。
   • 第一组的点 $i$ 再连接第二组中的一个点，转移 $f(i, s | (1 << j)) = \min(f(i, s | (1 << j)), f(i, s) + cost(i, j))$。这一步替代里算法 1 中的枚举子集。
4. 最终答案为 $f(n, (1 << m) - 1)$。

时间复杂度

• 状态数为 $O(n \cdot 2^m)$，转移时间为 $O(m)$，故总时间复杂度为 $O(nm \cdot 2^m)$。

空间复杂度

• 需要 $O(n \cdot 2^m)$ 的额外空间存储状态。

C++ 代码

class Solution {
public:
    int connectTwoGroups(vector<vector<int>>& cost) {
        const int n = cost.size(), m = cost[0].size();
        const int INF = 1000000000;
        vector<vector<int>> f(n + 1, vector<int>(1 << m, INF));

        f[0][0] = 0;
        for (int i = 1; i <= n; i++)
            for (int s = 0; s < (1 << m); s++)
                for (int j = 0; j < m; j++) {
                    f[i][s | (1 << j)] = min(f[i][s | (1 << j)],
                                             f[i - 1][s] + cost[i - 1][j]);

                    f[i][s | (1 << j)] = min(f[i][s | (1 << j)],
                                             f[i][s] + cost[i - 1][j]);
                }

        return f[n][(1 << m) - 1];
    }
};