题目描述

给你一个数组 rectangles，其中 rectangles[i] = [x_i, y_i, a_i, b_i] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (x_i, y_i)，右上顶点是 (a_i, b_i)。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true；否则，返回 false。

样例

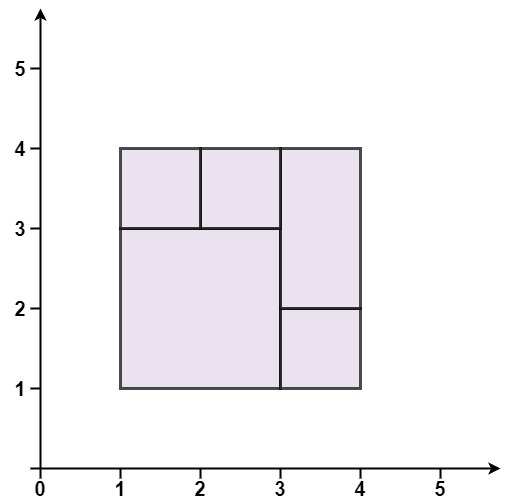
输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。 

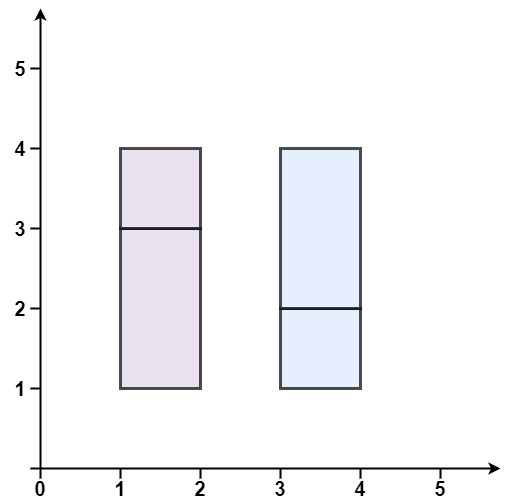
输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

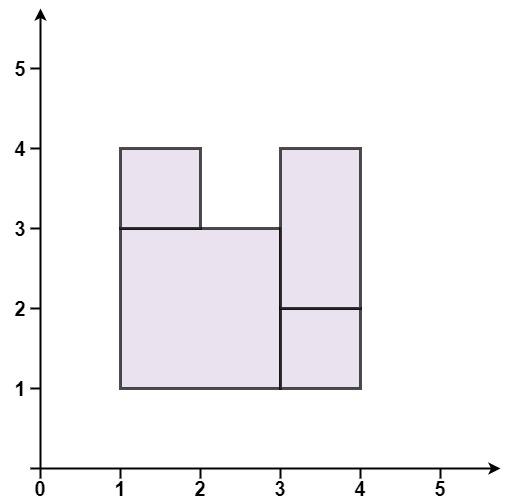
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出：false
解释：图形顶端留有空缺，无法覆盖成一个矩形。

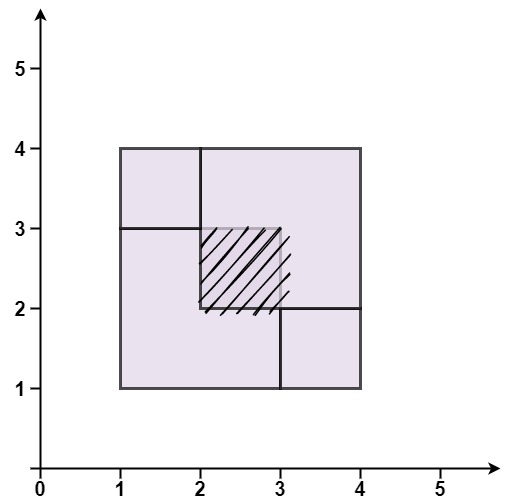
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

限制

• 1 <= rectangles.length <= 2 * 10^4
• rectangles[i].length == 4
• -10^5 <= x_i, y_i, a_i, b_i <= 10^5

算法

(排序，扫描线) $O(n \log n)$

1. 将每个矩形看做两条竖直的线段，左侧的线段权值为 $1$，右侧的线段权值为 $-1$。
2. 将这些线段按照横坐标从小到大排序，横坐标相同的，按照纵坐标从小到大排序。
3. 对于每一个有线段的横坐标，除了开头和末尾，其余横坐标必须保证，线段不重叠，且连通成一条直线。
4. 具体做法如下，对于每个横坐标上的线段，用两个数组分别记录权值为 -1 的线段和权值为 1 的线段。由于线段都是排好序的，所以重叠很容易判断。能连通一条直线的充分必要条件是，减少的线段需要和增加的线段看起来一样。
5. 这里看起来一样可以理解为，我们把首尾相邻的线段们看做一条线段，最后比较两个数组线段个数和线段端点是否都一致。
6. 最后还需要判断开头和末尾为只包含一条线段。

时间复杂度

• 排序的时间复杂度为 $O(n \log n)$，排序后，每个线段仅遍历一次，故总时间复杂度为 $O(n \log n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储所有的线段。

C++ 代码

struct Line {
    int x, y1, y2, v;
    Line(int x_, int y1_, int y2_, int v_):x(x_), y1(y1_), y2(y2_), v(v_){}
};

class Solution {
private:
    bool insert(vector<pair<int, int>> &seg, int l, int r) {
        if (seg.empty() || l > seg.back().second) {
            seg.emplace_back(l, r);

            return false;
        }

        if (l < seg.back().second)
            return true;

        seg.back().second = r;

        return false;
    }

public:
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        vector<Line> lines;
        for (const auto &r : rectangles) {
            lines.push_back(Line{r[0], r[1], r[3], 1});
            lines.push_back(Line{r[2], r[1], r[3], -1});
        }
        sort(lines.begin(), lines.end(), [](const Line &a, const Line &b) {
            if (a.x != b.x)
                return a.x < b.x;

            return a.y1 < b.y1;
        });

        const int n = lines.size();
        int last = 0;

        for (int i = 1; i <= n; i++) {
            if (i < n && lines[i].x == lines[i - 1].x)
                continue;

            vector<pair<int, int>> seg1, seg2;
            for (int j = last; j < i; j++) {
                bool is_overlap;

                if (lines[j].v == 1)
                    is_overlap = insert(seg1, lines[j].y1, lines[j].y2);
                else
                    is_overlap = insert(seg2, lines[j].y1, lines[j].y2);

                if (is_overlap)
                    return false;
            }

            if (last == 0 && seg1.size() > 1)
                return false;

            if (i == n && seg2.size() > 1)
                return false;

            if (last > 0 && i < n) {
                if (seg1.size() != seg2.size())
                    return false;

                for (int j = 0; j < seg1.size(); j++)
                    if (seg1[j] != seg2[j])
                        return false;
            }

            last = i;
        }

        return true;
    }
};