LeetCode 124. Binary Tree Maximum Path Sum

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

LeetCode 124. Binary Tree Maximum Path Sum 原题链接困难

作者：

yxc , 2018-05-29 02:27:06 , 所有人可见 , 阅读 4255

21

9

题目描述

给定一个非空二叉树，找到路径权值和的最大值。
在这道题目中，路径是指从树中某个节点开始，沿着树中的边走，走到某个节点为止，路过的所有节点的集合。
路径的权值和是指路径中所有节点的权值的总和。

样例1

输入：[1,2,3]

       1
      / \
     2   3

输出：6

样例2

输入：[-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出：42

算法

(递归，树的遍历) $O(n^2)$

树中每条路径，都存在一个离根节点最近的点，我们把它记为割点，用割点可以将整条路径分为两部分：从该节点向左子树延伸的路径，和从该节点向右子树延伸的部分，而且两部分都是自上而下延伸的。如下图所示，蓝色的节点为割点：
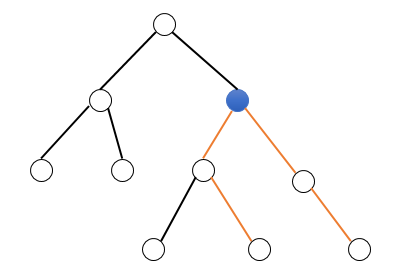
QQ图片20180529022450.png

我们可以递归遍历整棵树，递归时维护从每个节点开始往下延伸的最大路径和。
对于每个点，递归计算完左右子树后，我们将左右子树维护的两条最大路径，和该点拼接起来，就可以得到以这个点为割点的最大路径。
然后维护从这个点往下延伸的最大路径：从左右子树的路径中选择权值大的一条延伸即可。

时间复杂度分析：每个节点仅会遍历一次，所以时间复杂度是 $O(n)$。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int ans;
    int maxPathSum(TreeNode* root) {
        ans = INT_MIN;
        dfs(root);
        return ans;
    }

    int dfs(TreeNode* root)
    {
        if (!root) return 0;
        int left = max(0, dfs(root->left));
        int right = max(0, dfs(root->right));
        ans = max(ans, left + root->val + right);
        return root->val + max(left, right);
    }
};

17 评论

天道酬勤_58 2021-07-11 13:23

yls,我想问下如果让打印最长路径是什么的话怎么做呢。

jieHeEternity 2022-12-07 19:36

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int num = -1010;
    int max_ans=INT_MIN;

    int maxPathSum(TreeNode* root) {

        if(root == nullptr)return 0;
        int left=0,right=0;
        if(root->left)left=maxPathSum(root->left);
        if(root->right)right=maxPathSum(root->right);

        if(root->left==nullptr&&root->right==nullptr)
        {
              root->val;
        }
        else if(root->left==nullptr)
        {
            return max(root->val,max(right,right+root->val));
        }
        else if(root->right==nullptr)
        {
            return max(root->val,max(left,left+root->val));
        }
        // left,right,root->val,left+root->val,right+root->val,left+right+root->val;

        return max(max(max(max(max(left,right),root->val),left+root->val),right+root->val),left+right+root->val);

        // return max(max(right,left),left+right+root->val);




    }
};

代码这么写为什么不对啊？