题目描述

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

样例

输入：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}

输出：{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}

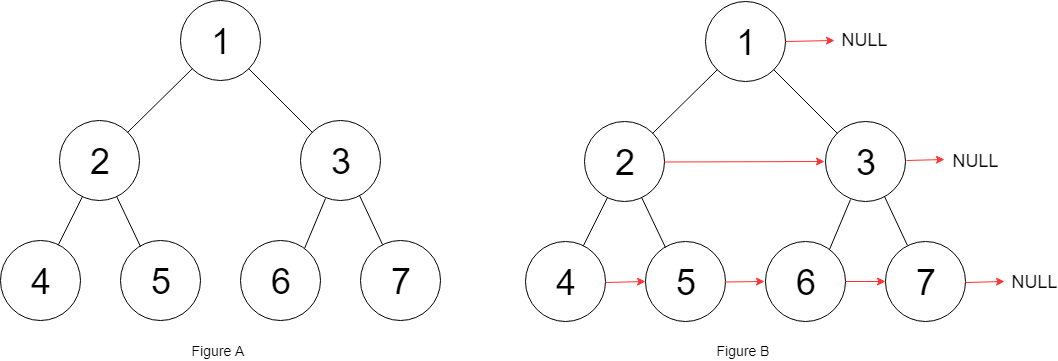
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。

算法1

时间复杂度 $O(n)$

根据题设条件，该二叉树为完美二叉树除叶子结点外所有节点存在左右子树，且叶子结点位于同一层。
利用next指针，节省层序遍历队列$O(n)$空间复杂度的消耗。

遍历每一层所有节点，当前层最左节点cur，当前遍历节点为p，
（1）若p.left不为空，则必然p.right存在，即p.left.next = p.right;
（2）若p.next不为空，则p.next必然存在左右子树，即p.right.next = p.next.left;
（3）若p.next为空，则p.right.next = null;
（4）此时二叉树当前层遍历完成，遍历下一层，起始节点为当前层最左节点的左子节点，即cur = cur.left;
（5）当cur.left为空，说明当前层为叶子结点，结束循环。

所有节点共被遍历一次，因此时间复杂度$O(n)$

Java 代码

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if (root == null) return null;
        Node cur = root;
        while (cur.left != null){
            for (Node p = cur; p != null;p = p.next){
                p.left.next = p.right;
                if (p.next != null)
                    p.right.next = p.next.left;
                else
                    p.right.next = null;
            }
            cur = cur.left;
        }
        return root;
    }
}