分析：

总体的思路：

按照体积来划分，把每个子树看作一个物品组，即每个以子树为根的一块中体积多少来划分
通过深搜考虑当前当前节点和他的子节点的关系。

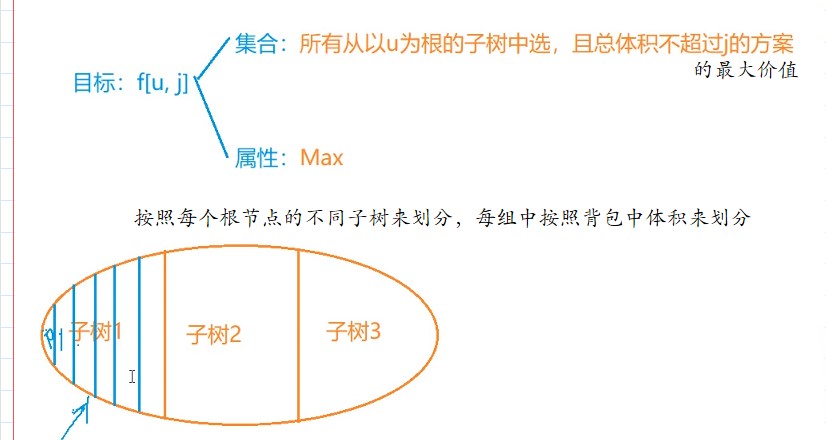
如果还是按照选或者不选的方案来划分，那么一共会有2^n中方案（深搜），数组无法存下，因此按照体积来划分，把每个子树看作一个物品组，即每个以子树为根的一块中体积多少来划分。
把方案数归类，提高效率

状态表示：

求一个物品组中指定体积v的方案f[u][k] k: 1 ~ v
当前树组给定体积 k 的最大价值等于它的子树组的给定体积 k 的最大价值+ 除了子树组的对应体积(j - k)的方案数
$\cal{f[u][k] = max(f[u][k], f[son][k] + f[u][j - k])}$

P.S

Question:
1.最后背包中还要加上当前根节点？
P.S：题目限制了必须要放当前点的父节点，如果背包的体积连父节点都放不进去，那么就不能当前子节点
（需要加上吗？需要，否则会出现没有存放父节点却存放了子节点的情况）

2.可以用有依赖的背包问题的思路来求吗？
不行，今明那道题是按照 子节点的不同选取方式的 方案来划分，题目规定了最多只有两个子节点
而这道题一个父节点可能有100个字节点（可能有2^100中方案），因此要按照体积来划分（一棵子树内部的体积一共是1 ~ m，那么一共有m + 1中选法）

3.为什么先计算不带父节点的情况，再加上父节点呢？
题目要求，必须要加上父节点，因此每次计算的时候，一定要把父节点加上f[root][i]= f[root][i − v[root]]+ w[root]
注意不是max，而是直接赋值

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int f[N][N];
int e[N], ne[N], h[N], idx;
int v[N], w[N],V;
void add(int a, int b)
{
    e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
}

void dfs(int root)
{
    //cout << h[-1] <<endl;
    for(int i = h[root]; i != -1; i = ne[i])
    {
     //    cout << root << " " << e[h[root]] << endl;
        int j = e[i];
        dfs(j);
        /*没有计算树根的体积*/
        for(int k = V - v[root]; k >= 0 ;k--)
        {
            for(int m = 1; m <= k; ++m)
                f[root][k] = max(f[root][k], f[j][m] + f[root][k - m]);
        }
    }
    /*计算每个子树组的体积的时候把当前树根的体积也算进去*/
    for(int i = V; i >= v[root]; i--)f[root][i] = f[root][i - v[root]] + w[root];
    /*题目限制了必须要放当前点的父节点，如果背包的体积连父节点都放不进去，那么就不能当前子节点*/
    for(int i = 0; i < v[root]; ++i)f[root][i] = 0;
}

int main()
{
    memset(h, -1, sizeof h);
    int N, root; cin >> N >> V;
    for(int i = 1; i <= N; ++i)
    {
        int p; cin >> v[i] >> w[i] >> p;
        if(p == -1)root = i;
        else add(p, i);
       // cout << h[-1] <<endl;
    }
    dfs(root);
    cout <<f[root][V] <<endl;
    return 0;
}