题目描述

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [fromi, toi] ，表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

样例

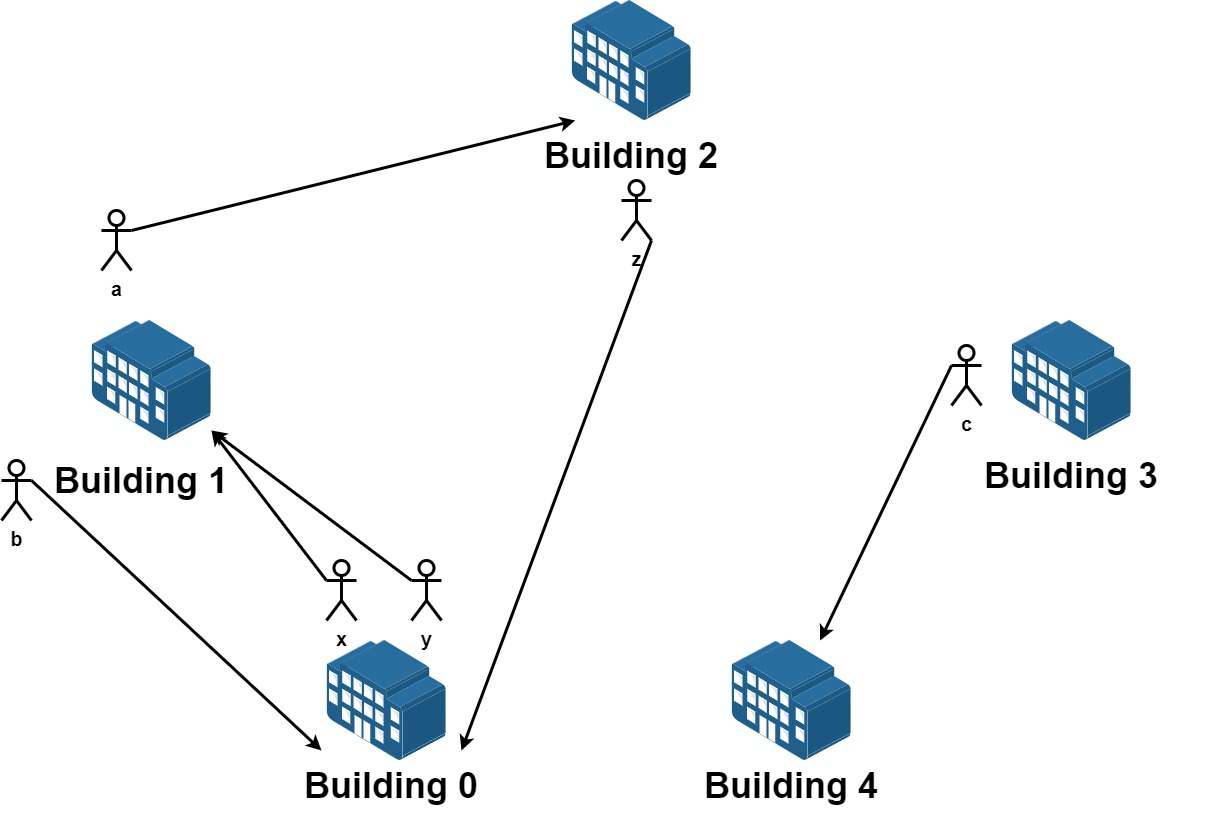
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

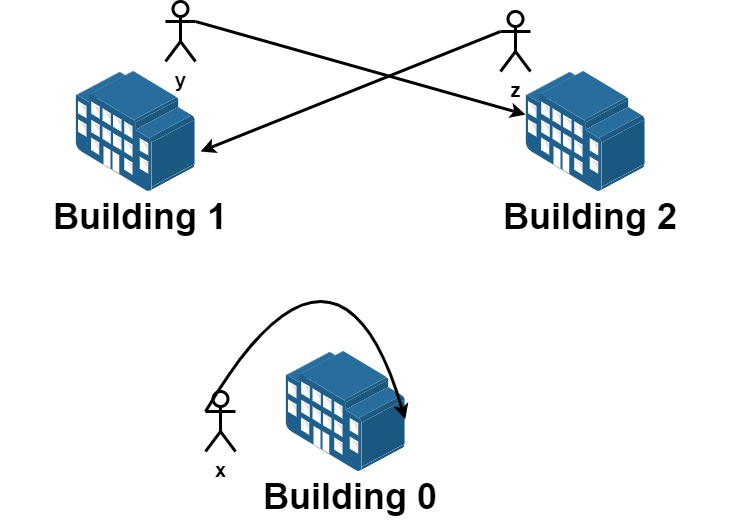
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

输入：n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出：4

算法分析

模拟 + 位运算

• 1、题目说到：从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 ，在满足某些部分人请求的情况下，一定会使得每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目
• 2、先看数据范围，最多只有16个请求，其中每个请求有允许 和 不允许两个状态，因此总的情况最多是2^16种
• 3、枚举所有请求允许和不允许的所有情况，当枚举到第i种状态时，第j位是1表示，表示第j个条件满足。其中cnt表示i状态有多少个1，并且记录每栋楼进入in的所有人数，和出去out的所有人数，但每栋楼k都满足in[k] == out[k]时，则表示当前状态i满足题意，用cnt更新ans

时间复杂度 $O(2^m * max(n, m))$

Java 代码

class Solution {
    public int maximumRequests(int n, int[][] requests) {
        int m = requests.length;
        int[] out = new int[n];//记录每栋楼出去多少人
        int[] in = new int[n];//记录每栋楼进来多少人
        int ans = 0;
        for(int i = 0;i < 1 << m;i ++)
        {
            Arrays.fill(out, 0);
            Arrays.fill(in, 0);
            int cnt = 0;
            for(int j = 0;j < m;j ++)
            {
                if((i >> j & 1) == 1)
                {
                    cnt ++;
                    out[requests[j][0]] ++;
                    in[requests[j][1]] ++;
                }
            }
            boolean flag = true;
            for(int j = 0;j < n;j ++)
            {
                if(out[j] != 0 && out[j] != in[j]) 
                {
                    flag = false;
                    break;
                }
            }
            if(flag) ans = Math.max(ans, cnt);
        }

        return ans;
    }
}