题意还是很好理解的，做法很巧妙，不太好实现。

题目描述

• 给定一个数轴，数轴上有 $n$ 个点 $a_{1\cdots n}$
• 从中选出 $k$ 对点（共 $2k$ 个），使 $k$ 对点之间的距离之和最小，求最小总长度。
• $2\le n\le 100000$

样例

n=5
k=2
1 3 4 6 12

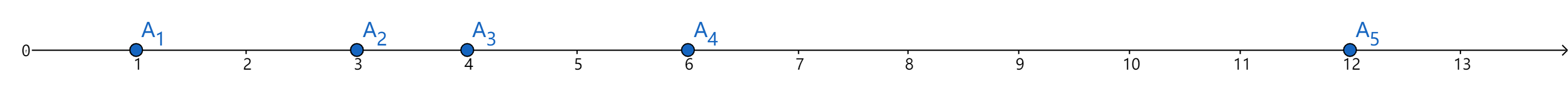
当第 $1$ 对取 $1$ 和 $3$，第 $2$ 对取 $4$ 和 $6$ 时，答案为最小值 $4$。

通过简单的观察后可以得到两个性质。

性质 $1$：所选的点对之间的是不可能存在重叠部分的。

因为假设有两对点对存在重叠部分，那么选取这 $4$ 个点中较小的 $2$ 个构成点对和较大的 $2$ 个构成点对，会构成 $2$ 对新的没有重叠部分的点对，答案会比原来更优。

举个栗子就是，如果原来第 $1$ 对取 $1$ 和 $6$，第 $2$ 对取 $3$ 和 $4$ ，存在重叠部分，将它们变为，第 $1$ 对取 $1$ 和 $3$，第 $2$ 对取 $4$ 和 $6$ ，不存在重叠部分，答案会变得更优。

性质 $2$：所选点对一定是相邻的。

因为如果所选点对不相邻，将所选点对改为相邻，答案会变得更优。

举个栗子，如果选择的是$1$ 和 $4$，改为$1$ 和 $3$，会变得更优。

得到这 $2$ 个性质后我们就可以对原数组进行差分，令 $d_i=a_i-a_{i-1}$

把相邻两个建筑物之间的距离抽象成一个点。

那么问题就可以转化为：

• 给出 $n-1$ 个点，每个点的权值分别为 $d_{1\cdots{n-1}}$
• 从中选出 $k$ 个不相邻的点，使 $k$ 个点的点权之和最小，求点权的最小总和。
• $2\le n\le 100000$

再看一下样例

那么答案就是选第一个和第三个点，答案为 $2+2＝4$

通过猜测我们可以想到这样一种贪心做法：每次选与已经选了的点不相邻的权值最小的点。

模拟一下样例，先选权值为 $1$ 的二号点，然后一号点和三号点就不能再选了，于是只能选四号点。

答案为 $1+6=7$，显然不是最优解，这种方法是错误的。

但是我们要分析这种方法到底哪里出了问题，我们选了二号点，之后就把选一号点和三号点的决策排除在外，实际上选一号点和三号点是有可能成为最优解的。

接下来从小到大考虑 $k$ 的取值

当 $k=1$ 时，答案显然为 $\min(d_i)$

当 $k=2$ 时，由之前的贪心做法进行改进，有两种可能

设最小值 $d_m=\min(d_i)$

第一种可能是，取 $d_m$ 和毫不相关的一个点

第二种可能是，同时取 $d_{m-1}$和 $d_{m+1}$

第一种情况很显然，第二种情况需要一些证明

证明：

假设第一个点取 $d_{m-1}$ ，第二个点不取 $d_{m+1}$ 更优

那么因为 $d_m$ 和 $d_{m+1}$ 都不能取，就只能取毫不相关的一个点 $d_x$，而又因为 $d_m$ 为最小值，那么 $d_m<d_{m-1}$，可以得到 $d_m+d_x<d_{m-1}+d_x$，则取 $d_m$ 和 $d_x$ 更优，与假设矛盾。

同理第一个点取 $d_{m+1}$ 时也可得证。

Q.E.D.

当 $k=3$ 时，也是有两种可能

第一种可能是，取 $d_{m-1},d_{m+1}$ 和毫不相关的一个点

第二种可能是，同时取 $d_{m-2},d_m$和 $d_{m+2}$

第一种情况也很显然，接下来证明第二种情况

证明：

假设第一个点选 $d_{m-2}$，但是不取 $d_{m+2}$ 时更优

那么我们发现 $d_{m-2},d_{m-1},d_{m+2}$ 都不能都选，剩下的是 $d_m,d_{m+1}$，所以至少要从边上选一个毫不相关的点 $d_x$，那么有贪心思想可知，剩下的一个点一定选 $d_m$，那么这时的答案为 $d_{m-2}+d_m+d_x$，但是当 $k=2$ 时的最优情况为 $d_{m-1}+d_{m+1}$，所以 $d_{m-1}+d_{m+1}<d_{m-2}+d_m$ ， 同时加 $d_x$ 可以得到 $d_{m-1}+d_{m+1}+d_x<d_{m-2}+d_m+d_x$，所以取 $d_{m-1}+d_{m+1}+d_x$ 时更优，与假设矛盾。

同理先取其他点时也可得证。

Q.E.D.

根据以上可以做出猜想：如果存在一段已经被连续（「连续」指隔一个点）选择的点，如果破坏其中任意一个点，那么会把所有点的选择情况进行翻转。

也就是说所有隔一个点连续的边是共进退的，有福同享，有难同当，要么都选，要么都不选，就比如说选择了 $d_{m-2},d_m,d_{m+2}$ 那么如果破坏了其中任意一个点，之后的选择情况就为 $d_{m-3},d_{m-1},d_{m+1},d_{m+3}$

如何证明这个猜想是对的呢，就要用到数学归纳法。

题外话，之前在《具体数学》中看到了关于数学归纳法的比喻，特别的形象贴切。

通过证明我们可以爬到梯子的最底一级（基础），并能从一个阶梯爬到上一个阶梯（归纳），数学归纳法就证明了：我们可以在一架梯子上想爬多高就爬多高.

回归正题。

证明：

basis：当 $k=1$ 时取最小值，显然成立。

induction：假设取 $k$ 个点时成立，取 $k+1$ 个点时，如果破坏了其中任意一个点，而不隔一个点连续进行选择，得到的结果更优。

那么绝对会选一些和这段毫不相关的点，不妨设为 $t$ 个，我们只需要把这 $t$ 个点中选 $t-1$ 个和这一段中已经选了的点替换为 $k$ 个时的情况，再加上 $t$ 个点剩下的 $1$ 个点，绝对会比之前更优，与假设矛盾。

Q.E.D.

好的！得到这条性质后，我们接着看应该怎么实现。

考虑每次递推 $k$ 时，答案 $ans$ 的增量。

$k=1$ 时 ，$ans＝d_m$

$k=2$ 时 ，$ans$ 相比 $k=1$ 时增加了 $d_{m-1}+d_{m+1}-d_m$

$k=3$ 时 ，$ans$ 相比 $k=2$ 时增加了 $d_{m-2}+d_m+d_{m+2}-d_{m-1}-d_{m+1}$，恒等变形后为 $d_{m-2}+d_{m+2}-(d_{m-1}+d_{m+1}-d_m)$

可以发现，括号里正是上一种情况的值。

所以最终的做法就是每次找到最小值 $d_i$，把它计入答案，然后把它 $i$ 和它的左面的点 $l(i)$ 和右面的点 $r(i)$ 删除，然后把点 $i$ 赋一个新的权值，$d_i\gets d_{l(i)}+d_{r(i)}-d_i$，然后再把 $i$ 插入候选集合。

因为我们需要插入和删除，所以就用一个平衡树来维护答案集合，因为要知道每个点的左面的点和右面的点，所以就用一个双向链表来维护。

而每个元素最多插入和删除 $k$ 次，又因为 $n$ 和 $k$ 是同阶的，所以最终时间复杂度是 $O(n\log n)$