先简单复习一下学习AC自动机所需要的前缀知识。
前缀知识 1-Trie树
字典树,也称Trie树,前缀树,主要用于存储大量的字符串以及查询操作。
对于Trie树,一般有两个操作:
- 1.insert操作,在Trie树中存储一个字符串
- 2.query操作,在Trie树中查询一个字符串
举个例子,对于这样几个字符串,{abcde,abcgf,hello,her}我们看他们在Trie树中是如何存储的:
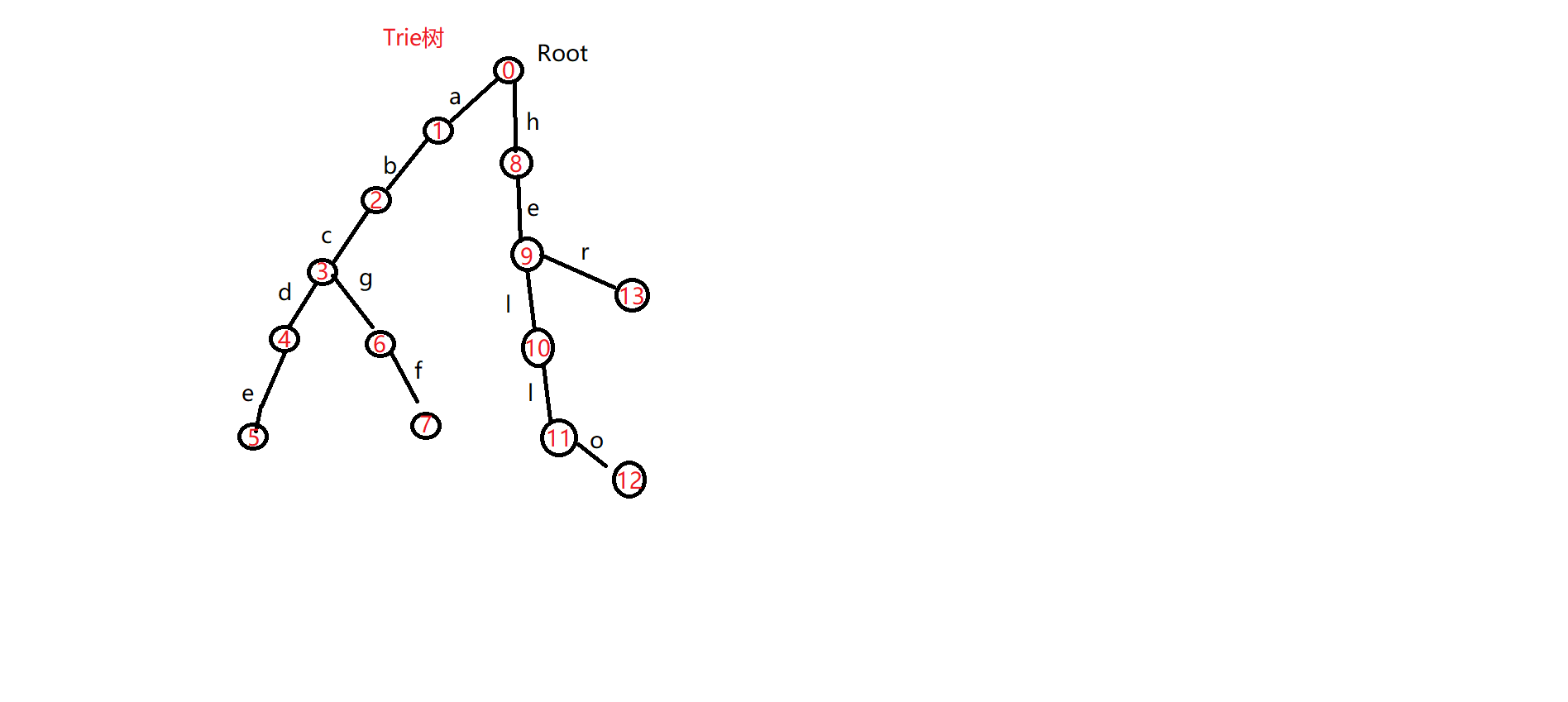
这里需要注意,字符是边,而不是节点,但都是一一对应的
代码
int son[N][26],cnt[N],idx; //cnt数组记录以当前节点为结尾的字符串的数目,idx为节点编号
int n;
void insert(string& s){
int n = s.length();
int p = 0;
for(int i = 0; i<n; i++){
int u = s[i]-'a';
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
cnt[p] ++;
}
int query(string &s){
int p = 0;
int n = s.length();
for(int i = 0; i<n; i++){
int u = s[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
前缀知识2 - KMP算法
对于KMP算法的介绍网上有很多优秀的博客,这里就不再赘述了。。。
在学习了Trie树和KMP算法后,我们就可以学习AC自动机了。
这里放个B站的视频链接,我觉得讲得很清楚–>轻松掌握AC自动机
AC自动机(Aho-Corasick automaton)
了解:我们知道KMP算法是解决单模式串的匹配问题的,而AC自动机是用来解决多模式串匹配问题的。
对于多模式串的存储,我们就可以用到Trie树来存储,在匹配过程中,一旦发生失配,我们应该如何处理呢?在KMP算法中,我们对模式串构建了next数组,在失配时通过next数组来加速匹配过程,那在Trie树中,我们是不是也可以通过一个数组来维护前缀和后缀的某些信息呢?
fail数组
定义:对于Trie树中当前某个节点i,若fail[i]=j表示Trie树中到j为止的字符串是到i为止的字符串的最长后缀。
一张图看懂fail数组:为了避免图片过乱,对于fail[i] = 0的点(即指向root的点)均未画出
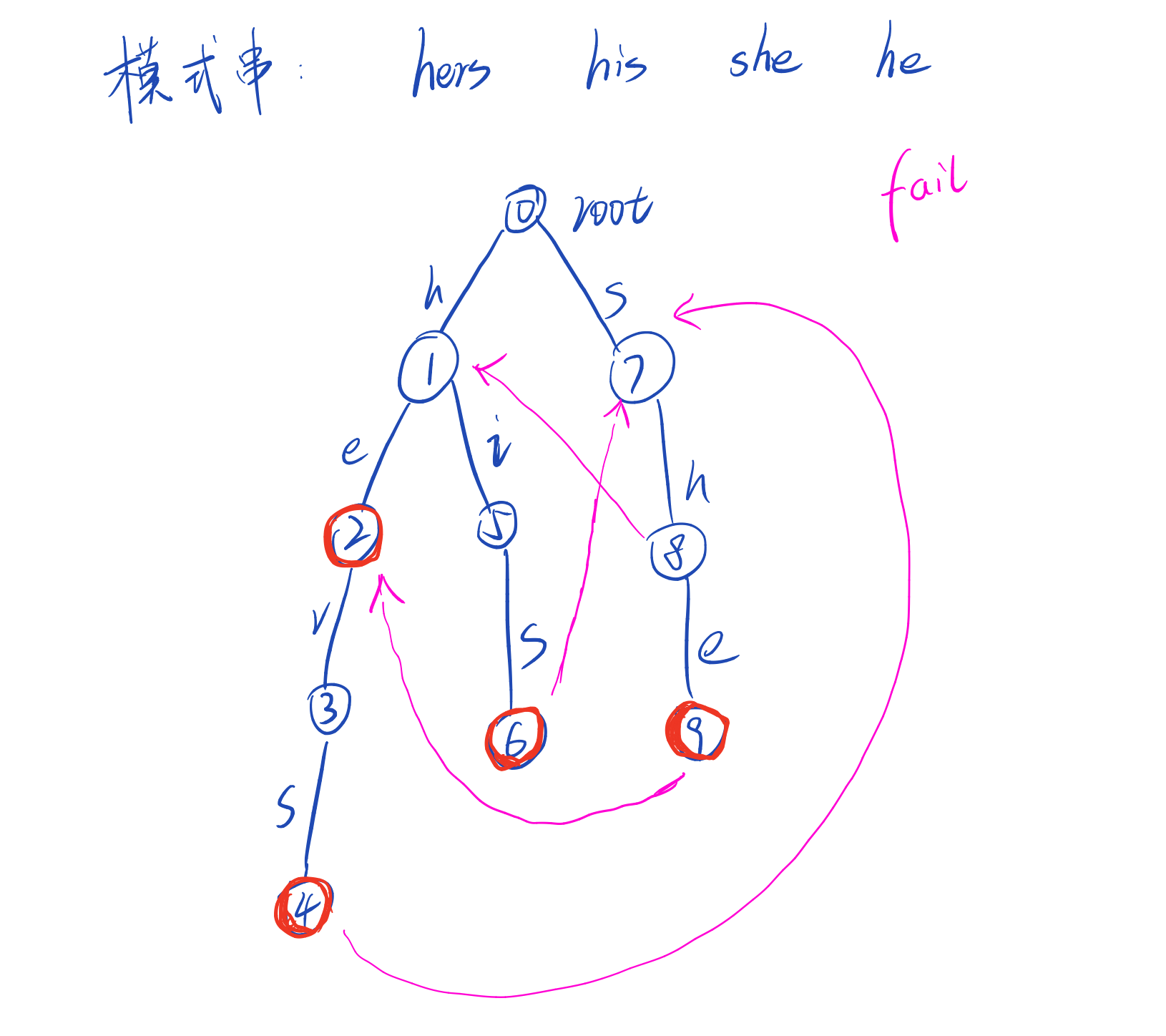
有了这个fail数组后,我们模拟一个简单的样例,比如当前主串是uhershef
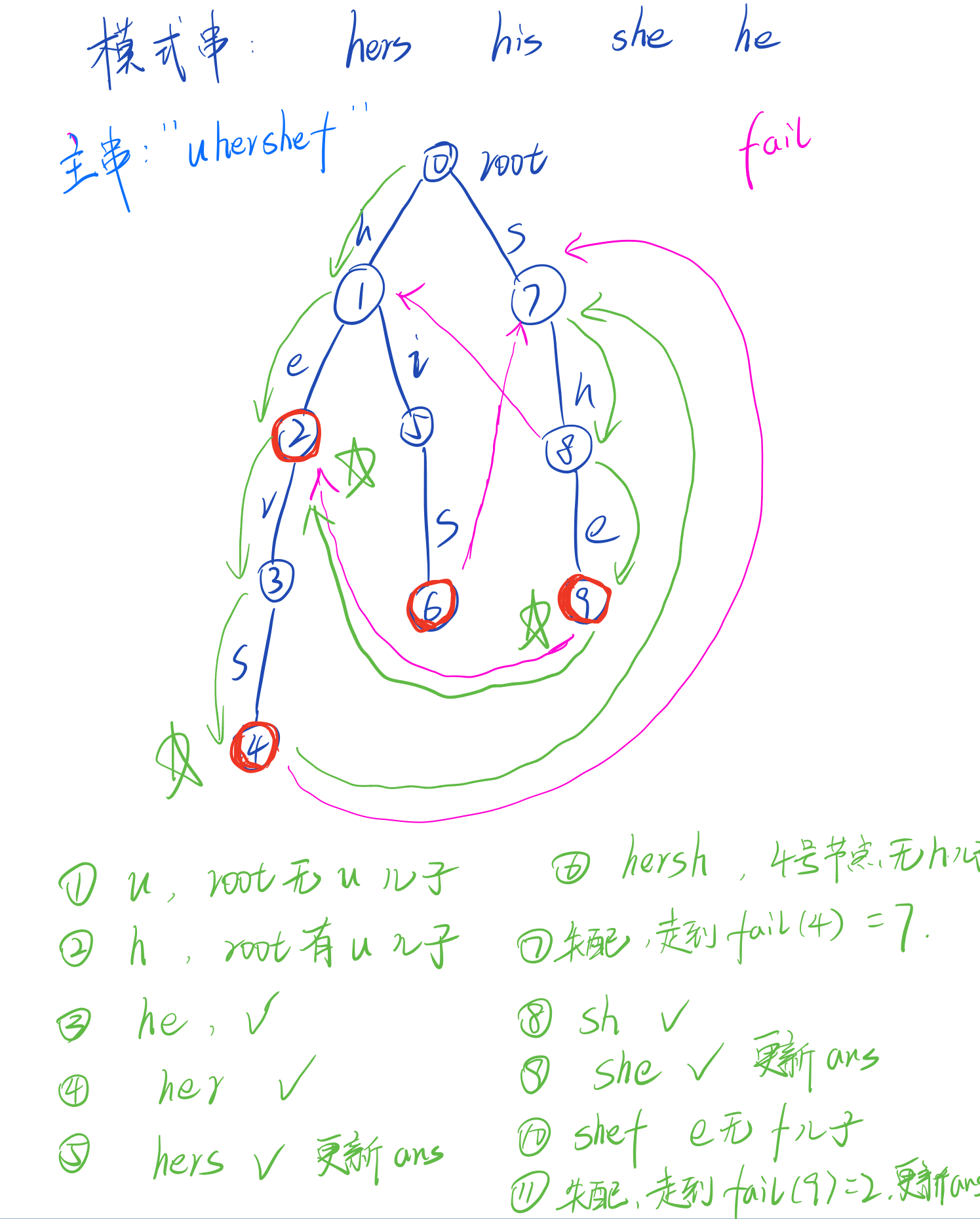
大家可以自己模仿样例在纸上画一下过程,在理解了这个过程之后,其实fail数组也就不再那么神秘了,当我们在一个分支上走不下去了之后,我们不必头铁,可以换个方向继续往下走,而fail数组的作用就是这样,当发生失配时,我们可以通过预处理出的fail数组告诉我们其他分支的信息(即满足当前字符串最长后缀的节点),然后继续向后遍历即可。
如何求fail数组
在Trie树建好之后,我们如何给这棵树添加信息即如何预处理出fail数组,其实仔细观察第一幅图我们就可以看出来,我们可以利用前一层的信息来更新下一层的节点信息,那么我们可以用BFS来一层一层地扩展。
代码如下:
void build(){
int hh = 0, tt = -1;
for(int i = 0; i<26; i++){
if(tr[0][i]) q[++tt] = tr[0][i]; //第一层的所有节点一定指向root
}
while(hh<=tt){
int t = q[hh++];
for(int i = 0; i<26; i++){
int c = tr[t][i];
//利用父节点的信息来更新自己的
if(!c) tr[t][i] = tr[fail[t]][i]; //将树填充为图,这里可以通过测试样例测试一下
else{
fail[c] = tr[fail[t]][i];
q[++tt] = c;
}
}
}
}
强烈建议大家画个图自己模拟一遍,绝对比直接对照代码看有效!!
匹配
匹配的过程在第二张图里面已经提及到了,大致过程如下,从根节点开始匹配,如果匹配,继续跳到下一个节点,如果失配,则跳到fail指针,然后继续匹配。
对于Trie图,我的个人理解是,利用fail指针来补充trie树的信息,使其成为一个图,然后在匹配过程中,我们无需考虑fail指针,直接令j = tr[j][t],这里其实就包括了t+'a'这个字符如果不存在时的情况,如果不存在,其实就等价于j = tr[fail[j]][t]。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4+100, L = 55, M = 1e6+100;
char str[M],s[L];
int tr[N*L][26], cnt[N*L],idx;
int fail[N*L],q[N*L];
int t,n;
//字典树建树过程
void insert(char s[]){
int p = 0;
for(int i = 0; s[i]; i++){
int t = s[i]-'a';
if(!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
cnt[p]++;
}
//宽搜预处理出fail数组以及trie子图
void build(){
int hh = 0, tt = -1;
for(int i = 0; i<26; i++){
if(tr[0][i]) q[++tt] = tr[0][i]; //第一层直接入队
}
while(hh<=tt){
int t = q[hh++];
for(int i = 0; i<26; i++){
int c = tr[t][i];
if(!c) tr[t][i] = tr[fail[t]][i];
else{
fail[c] = tr[fail[t]][i]; //利用上层信息更新现在的节点信息
q[++tt] = c;
}
}
}
}
int main()
{
scanf("%d",&t);
while(t--){
scanf("%d",&n);
memset(tr,0,sizeof tr);
memset(fail,0,sizeof fail);
memset(cnt,0,sizeof cnt);
for(int i = 1; i<=n; i++){
scanf("%s",s);
insert(s);
}
build();
scanf("%s",str);
int ans = 0;
for(int i = 0,j = 0; str[i]; i++){
int t = str[i] - 'a'; //当前遍历到的字符
j = tr[j][t];
int p = j;
while(p){
ans += cnt[p];//更新答案
cnt[p] = 0; //统计出现的种类,所以清空标记
p = fail[p]; //向上跳,不漏答案
}
}
printf("%d\n",ans);
}
return 0;
}

